- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:12.
- Zuletzt bearbeitet 2025-06-01 06:05.
Das Addieren und Subtrahieren von Brüchen ist eine wichtige Fähigkeit. Brüche tauchen im Alltag ständig auf, insbesondere im Mathematikunterricht, von der Grundschule bis zum College. Befolgen Sie diese Schritte, um zu erfahren, wie Sie Brüche von äquivalenten Brüchen, ungleichen Brüchen, gemischten Zahlen oder gewöhnlichen Brüchen addieren und subtrahieren. Wenn Sie einen Weg bereits kennen, ist es wirklich einfach, die anderen Brüche zu lösen!
Schritt
Methode 1 von 4: Addition und Subtraktion von Brüchen mit demselben Nenner
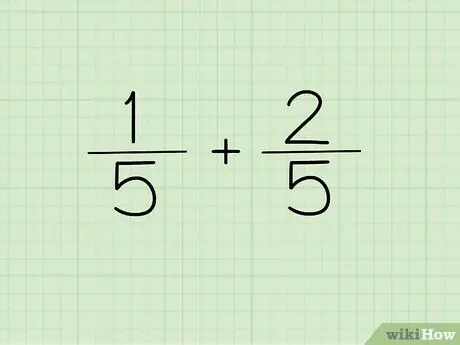
Schritt 1. Schreiben Sie Ihre Frage auf
Wenn der Nenner der beiden Brüche, die Sie addieren oder subtrahieren möchten, gleich ist, schreiben Sie den Nenner einmal als Nenner Ihrer Antwort auf.
Mit anderen Worten, 1/5 und 2/5 müssen nicht als 1/5 + 2/5 = ?, kann aber geschrieben werden als (1+2)/5 = ?. Die Nenner sind gleich, können also nur einmal geschrieben werden. Die beiden Zähler werden kombiniert
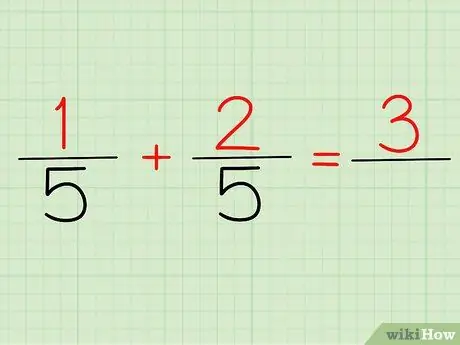
Schritt 2. Addieren Sie die Zähler
Der Zähler ist die Zahl, die über jedem Bruch steht. Wenn wir uns das obige Problem ansehen, sind 1/5 und 2/5, 1 und 2 unsere Zähler.
Egal, ob Sie 1/5 + 2/5 oder (1+2)/5 schreiben, Ihre Antwort ist dieselbe: 3! Denn 1 + 2 = 3

Schritt 3. Lassen Sie den Nenner
Da die Nenner gleich sind, machen Sie nichts mit den Nennern! Addieren, subtrahieren, multiplizieren oder dividieren Sie nicht. Kümmer dich nicht darum.
Aus dem gleichen Beispiel ist unser Nenner also 5. Richtig! 5 ist die unterste Zahl unserer Fraktion. Wir haben die halbe Antwort

Schritt 4. Schreiben Sie Ihre Antwort auf
Jetzt müssen Sie nur noch Zähler und Nenner aufschreiben! Wenn Sie das obige Beispiel verwenden, lautet Ihre Antwort 3/5.
Wie lautet dein Zähler? 3. Ihr Nenner? 5. Daher ist 1/5 + 2/5 oder (1+2)/5 gleich 3/5.
Methode 2 von 4: Addition und Subtraktion von Brüchen mit unterschiedlichen Nennern

Schritt 1. Finden Sie den kleinsten gemeinsamen Nenner
Das heißt, der kleinste Nenner ist für beide Brüche gleich. Angenommen, wir haben die Brüche 2/3 und 3/4. Was ist der Nenner? 3 und 4. Um den kleinsten gemeinsamen Nenner beider Brüche zu finden, können Sie dies auf drei Arten tun:
- Schreiben Sie die Vielfachen von auf. Vielfache von 3 sind 3, 6, 9, 12, 15, 18 … und so weiter. Vielfaches von 4? 4, 8, 12, 16, 20 usw. Was ist die kleinste Zahl, die ein Vielfaches der beiden ist? 12! Das ist der kleinste gemeinsame Nenner.
-
Primfaktorzerlegung. Wenn Sie sich mit Faktoren auskennen, können Sie eine Primfaktorzerlegung durchführen. Das heißt, Sie suchen nach den Zahlen, die Ihren Nenner bilden. Für die Zahl 3 sind die Faktoren 3 und 1. Für die Zahl 4 sind die Faktoren 2 und 2. Dann ihr alle. 3 x 2 x 2 = 12. Ihr kleinster gemeinsamer Nenner!
Multiplizieren Sie alle Zahlen mit der kleineren Zahl. Bei einigen Problemen wie diesem können Sie beide Zahlen multiplizieren - 3 x 4 = 12. Wenn Sie jedoch einen großen Nenner haben, tun Sie dies nicht! Sie möchten nicht 56 x 44 multiplizieren und alles geben, um 2.464 zu erhalten

Schritt 2. Multiplizieren Sie den Nenner mit der Zahl, die benötigt wird, um den kleinsten gemeinsamen Nenner zu erhalten
Mit anderen Worten, Sie möchten, dass alle Ihre Nenner gleich sind. In unserem Beispiel möchten wir, dass der Nenner 12 ist. Um 3 in 12 zu ändern, multiplizieren Sie 3 mit 4. Um 4 in 12 zu ändern, multiplizieren Sie 4 mit 3. Derselbe Nenner ist der Nenner Ihrer endgültigen Antwort.
-
Aus 2/3 wird also 2/3 x 4 und aus 3/4 wird 3/4 x 3. Das heißt, wir haben jetzt 2/12 und 3/12. Aber wir sind noch nicht fertig!
- Sie werden feststellen, dass die Nenner miteinander multipliziert werden. Dies ist in dieser Situation möglich, jedoch nicht in allen Situationen. Anstatt beide Nenner zu multiplizieren, können Sie manchmal beide Nenner mit einer anderen Zahl multiplizieren, um die kleinere Zahl zu erhalten.
- Dann müssen Sie bei anderen Problemen manchmal nur einen Nenner multiplizieren, um ihn gleich dem Nenner des anderen Bruchs in der Aufgabe zu machen.

Schritt 3. Multiplizieren Sie den Zähler mit derselben Zahl
Wenn Sie den Nenner mit einer Zahl multiplizieren, müssen Sie auch den Zähler mit derselben Zahl multiplizieren. Was wir im letzten Schritt gemacht haben, ist nur ein Teil der Multiplikation, die durchgeführt werden muss.
Wir haben 2/3x4 und 2/4x3 als ersten Schritt - dann im zweiten Schritt 2 x 4/3 x 4 und 3 x 3/4 x 3. Das heißt, unsere neuen Zahlen sind 8/12 und 9/ 12. Perfekt
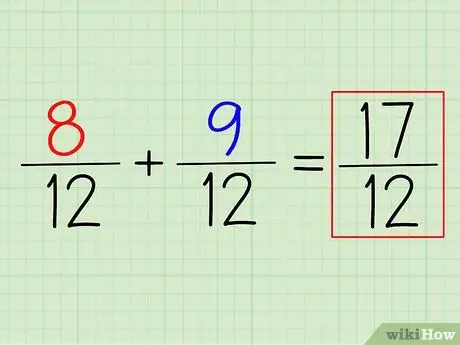
Schritt 4. Addieren (oder subtrahieren) Sie die Zähler, um die Antwort zu erhalten
Um 8/12 + 9/12 zu addieren, müssen Sie nur die Zähler addieren. Denken Sie daran: Lassen Sie einfach den Nenner. Der kleinste gemeinsame Nenner, den Sie finden, ist Ihr endgültiger Nenner.
In diesem Beispiel ist (8+9)/12 = 17/12. Um sie in eine gemischte Zahl umzuwandeln, subtrahiere einfach den Nenner vom Zähler und schreibe den Rest auf. In diesem Fall 17/12 = 1 5/12
Methode 3 von 4: Addieren und Subtrahieren von gemischten und gemeinsamen Brüchen
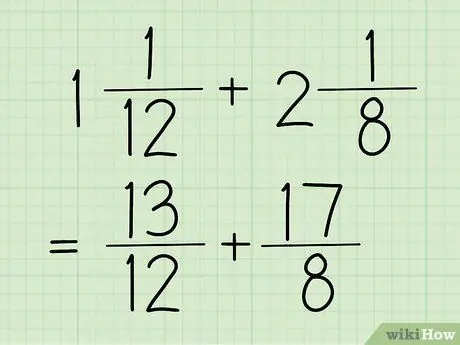
Schritt 1. Wandeln Sie Ihre gemischten Brüche in gewöhnliche Brüche um
Eine gemischte Zahl ist ein Bruch, der eine ganze Zahl und einen Bruch hat, wie im obigen Beispiel (1 5/12). Ein gewöhnlicher Bruch ist ein Bruch, dessen Zähler (obere Zahl) größer ist als der Nenner (untere Zahl). Dieser Bruch ist auch im vorherigen Schritt zu sehen, der 17/12 beträgt.
Für die Beispiele in diesem Abschnitt verwenden wir 13/12 und 17/8

Schritt 2. Finden Sie einen gemeinsamen Nenner
Erinnern Sie sich an die drei Möglichkeiten, den kleinsten gemeinsamen Nenner zu finden? Indem man Vielfache schreibt, die Primfaktorzerlegung verwendet oder die Nenner multipliziert.
Lassen Sie uns Vielfache unseres Beispiels 12 und 8 finden. Was ist die kleinste Zahl, die beide gemeinsam haben? 24. 8, 16, 24 und 12, 24 - Bingo

Schritt 3. Multiplizieren Sie Zähler und Nenner, um den entsprechenden Bruch zu finden
Beide Nenner müssen auf 24 geändert werden. Wie rechnet man 12 in 24 um? Mit 2 multiplizieren. 8 bis 24? Mit drei multiplizieren. Aber nicht vergessen - auch die Zähler müssen multipliziert werden!
Also (13 x 2)/(12 x 2) = 26/24. Und (17 x 3)/(8 x 3) = 51/24. Damit sind wir fast fertig

Schritt 4. Addieren oder subtrahieren Sie Ihre Brüche
Da Sie nun den gleichen Nenner haben, können Sie die beiden Zähler einfach addieren. Denken Sie daran, lassen Sie einfach den Nenner!
26/24 + 51/24 = 77/24. Das ist Ihre Summe! Die Zahlen oben waren jedoch zu groß…

Schritt 5. Wandeln Sie Ihre Antwort wieder in gemischte Zahlen um
Die sehr große Zahl oben im Bruch fühlt sich etwas seltsam an - Sie können die Größe Ihres Bruchs nicht erkennen. Alles, was Sie tun müssen, ist, Ihren Nenner so oft vom Zähler abzuziehen, bis er nicht mehr subtrahiert werden kann, und den Rest aufschreiben.
-
In diesem Beispiel 77 minus 24 mal 3 mal. Das heißt, 24 x 3 = 72. Der Rest ist 5! Also, was ist Ihr Endergebnis? 3 5/24.
So wahr!
Methode 4 von 4: Brüche addieren und subtrahieren, ohne LCM. zu finden
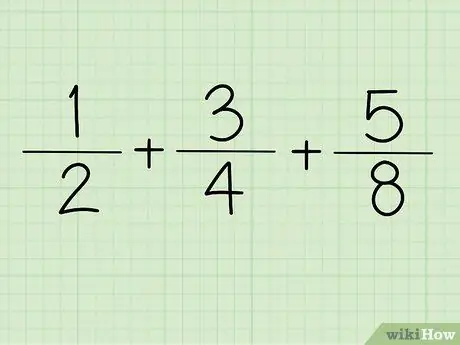
Schritt 1. Schreiben Sie den Bruch auf
Zum Beispiel + +

Schritt 2. Lösen Sie zuerst den Zähler
- Multipliziere mit dem Zähler des anderen Bruchs.
- Multiplizieren Sie 1 mit 4 und 8. [32]
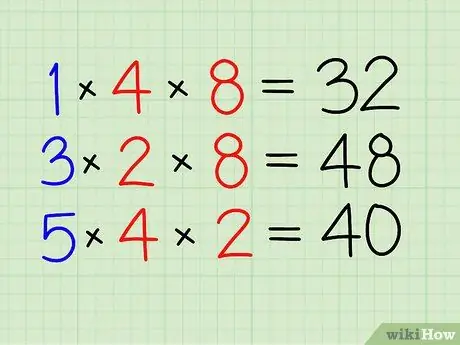
Schritt 3. Machen Sie dasselbe für die anderen Fraktionen
- Multiplizieren Sie 3 mit 2 und 8. [48]
- Zum Schluss multiplizieren Sie 5 mit 4 und 2. [40]
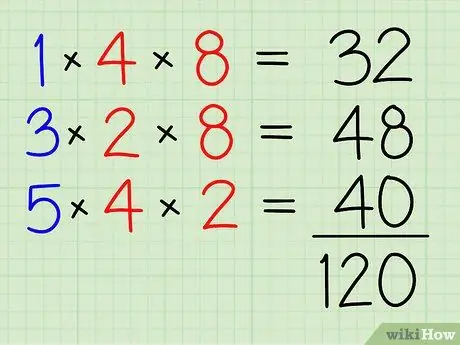
Schritt 4. Fügen Sie sie alle zusammen
32+48+40=120
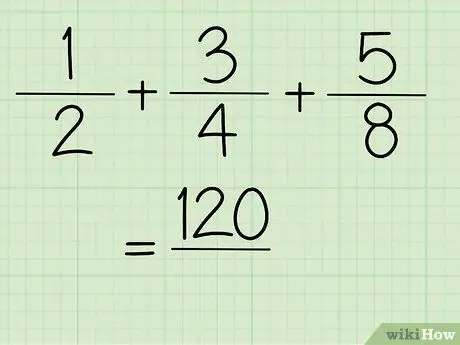
Schritt 5. Jetzt erhalten Sie den Zählerwert

Schritt 6. Lösen Sie den Nenner des Bruchs

Schritt 7. Multiplizieren Sie alle Nenner der Brüche
2×4×8=64

Schritt 8. Jetzt erhalten Sie das Ergebnis
120/64 = 1 56/64 = 1 ⅞
Warnung
- Mit dieser Methode können Sie große Zahlen multiplizieren.
- Möglicherweise benötigen Sie einen Taschenrechner, um auf diese Weise zu berechnen.






