- Autor Jason Gerald [email protected].
- Public 2023-12-16 11:03.
- Zuletzt bearbeitet 2025-01-23 12:14.
Für die meisten Menschen sind Brüche die ersten komplizierten Berechnungen, auf die sie stoßen. Das Konzept der Brüche ist ziemlich schwierig und erfordert, dass Sie spezielle Bedingungen lernen, um es zu tun. Da Brüche spezielle Regeln für Addition, Subtraktion, Multiplikation und Division haben, sind viele Leute darüber verwirrt. Mit viel Übung kann jedoch jeder Berechnungen im Zusammenhang mit Brüchen erlernen und vervollständigen.
Schritt
Methode 1 von 5: Brüche verstehen
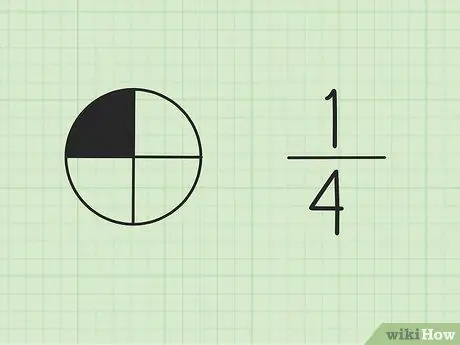
Schritt 1. Verstehe, dass Brüche Teil eines Ganzen sind
Die Zahl oben wird als Zähler bezeichnet und stellt die Anzahl der Teile der Gesamtsumme dar. Die untere Zahl wird als Nenner bezeichnet und repräsentiert die Gesamtzahl der Teile.
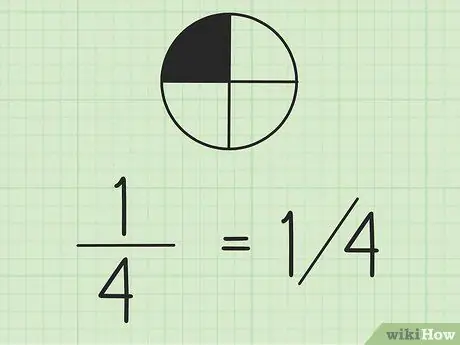
Schritt 2. Denken Sie daran, dass Sie Brüche mit Schrägstrichen schreiben können
Die linke Zahl ist der Zähler und die rechte Zahl der Nenner. Wenn Sie mit Brüchen in derselben Zeile arbeiten, empfiehlt es sich, den Zähler über den Nenner zu schreiben.
Nimmst du zum Beispiel eines von vier Pizzastücken, hast du Pizza. Wenn Sie 7/3 Pizzen haben, bedeutet dies, dass Sie zwei ganze Pizzen plus 1 von 3 Pizzastücken haben
Methode 2 von 5: Unterschied zwischen gemischten und einfachen Brüchen

Schritt 1. Verstehe, dass gemischte Zahlen aus ganzen Zahlen und Brüchen bestehen, zum Beispiel 2 1/3 oder 45 1/2
Normalerweise müssen Sie gemischte Zahlen in eine einfachere Form umwandeln, um addieren, subtrahieren, multiplizieren oder dividieren zu können.

Schritt 2. Ändern Sie die gemischte Zahl, indem Sie die ganze Zahl mit dem Nenner im Bruch multiplizieren und dann mit dem Zähler addieren
Schreiben Sie das Ergebnis als Zähler, während sich der Nenner nicht ändert.
Um beispielsweise 2 1/3 in einen einfachen Bruch umzuwandeln, multiplizieren Sie 2 mit 3, addieren Sie dann 1 und erhalten Sie 7/3

Schritt 3. Wandeln Sie einfache Brüche in gemischte Zahlen um, indem Sie den Zähler durch den Nenner dividieren
Das gesamte Ergebnis der Division wird als ganze Zahl geschrieben, und der Rest der Division wird als Zähler des Bruchs geschrieben. Der Nenner ändert sich nicht.
Um beispielsweise 7/3 in eine gemischte Zahl umzuwandeln, dividiere 7 durch 3, um 2 mit einem Rest von 1 zu erhalten. Die gemischte Zahl ist also 2 1/3. Einfache Brüche können nur in gemischte Zahlen umgewandelt werden, wenn der Zähler größer als der Nenner ist
Methode 3 von 5: Brüche addieren und subtrahieren
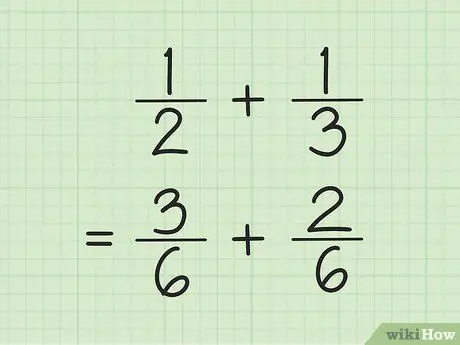
Schritt 1. Finden Sie einen gemeinsamen Nenner, um Brüche zu addieren und zu subtrahieren
Der Trick ist, die Zahlen im Nenner zu multiplizieren und dann jeden Zähler mit der Zahl zu multiplizieren, die verwendet wird, um den Nenner zu finden. Manchmal können Sie das LCM (kleinstes gemeinsames Vielfaches) für den Nenner finden, indem Sie die Nenner miteinander multiplizieren.
Um beispielsweise und 1/3 zu addieren, ermitteln Sie zunächst den LCM (kleinstes gemeinsames Vielfaches) der beiden Nenner, indem Sie sie miteinander multiplizieren. Daher multiplizieren Sie 2 und 3, um LCM 6 zu erhalten. Multiplizieren Sie 1 mit 3, um 3 als neuen Zähler des ersten Bruchs zu erhalten. Multiplizieren Sie 1 mit 2, um 2 als neuen Zähler des zweiten Bruchs zu erhalten. Ihre neuen Brüche sind 3/6 und 2/6
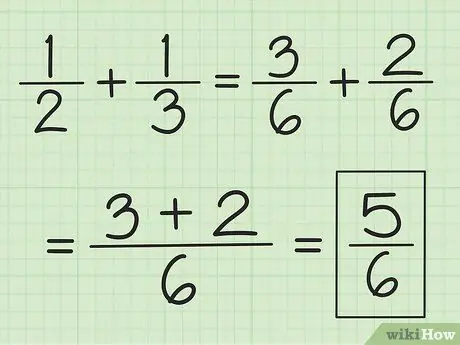
Schritt 2. Addieren Sie die beiden Zähler zusammen und ändern Sie den Nenner nicht
Zum Beispiel ist 3/6 plus 2/6 5/6 und 2/6 plus 1/6 ist 3/6
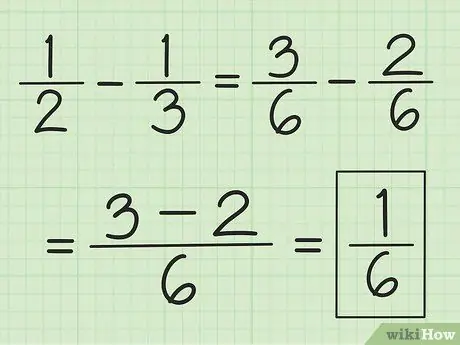
Schritt 3. Verwenden Sie eine ähnliche Technik für die Subtraktion
Finden Sie zuerst die LCM der Nenner, aber anstatt sie zu addieren, subtrahieren Sie die Zahl des ersten Zählers von der Zahl des zweiten.
Um zum Beispiel 1/3 von 1/2 zu subtrahieren, ändern Sie zuerst die Brüche in 3/6 und 2/6, dann subtrahieren Sie 3 von 2, um 1 zu erhalten. Dies ergibt 1/6
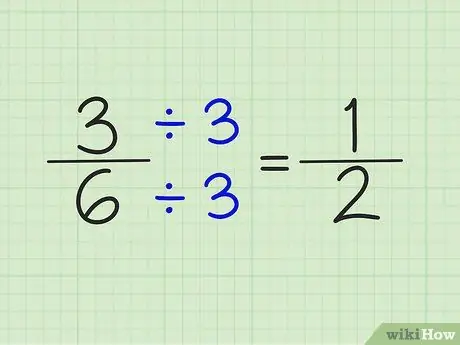
Schritt 4. Vereinfachen Sie Brüche, indem Sie Zähler und Nenner durch dieselbe Zahl dividieren
Zum Beispiel kann die Zahl 5/6 nicht vereinfacht werden. 3/6 kann jedoch vereinfacht werden, indem Zähler und Nenner durch die Zahl 3 geteilt werden. Das Ergebnis ist ein Bruch von 1/2

Schritt 5. Wandeln Sie den Bruch in eine gemischte Zahl um, wenn der Zähler größer als der Nenner ist
Methode 4 von 5: Brüche multiplizieren und dividieren
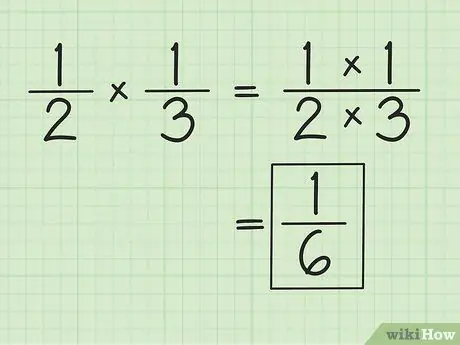
Schritt 1. Multiplizieren Sie Zähler und Nenner separat, um Brüche zu multiplizieren
Wenn Sie beispielsweise mit 1/3 multiplizieren, ist das Ergebnis 1/6 (1 mal 1 und 2 mal 3). Beim Multiplizieren von Brüchen müssen die Nenner nicht übereinstimmen. Vereinfachen oder ändern Sie die erhaltenen Ergebnisse, falls erforderlich
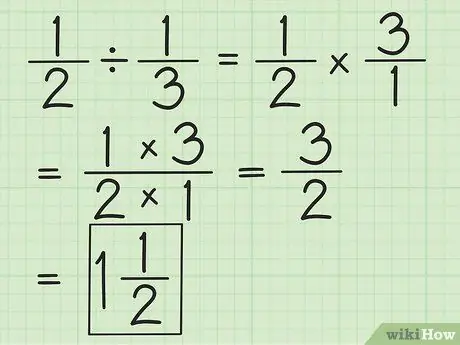
Schritt 2. Dividieren Sie zwei Brüche, indem Sie den zweiten Bruch invertieren und dann beide multiplizieren
Wenn Sie beispielsweise 1/2 durch 1/3 teilen möchten, kehren Sie zuerst den zweiten Bruch in 3/1 um. Multipliziere mit 3/1 und erhalte 3/2. Vereinfachen Sie Brüche oder konvertieren Sie sie in gemischte Zahlen, wenn möglich
Methode 5 von 5: Arbeiten mit komplexen Brüchen
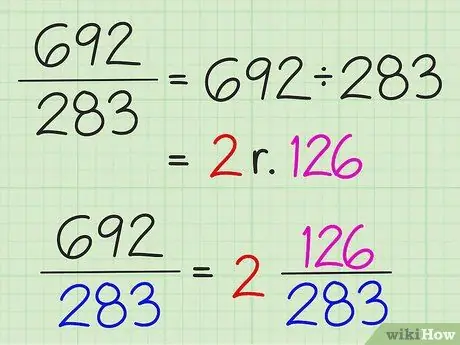
Schritt 1. Arbeiten Sie alle Brüche auf die gleiche Weise, auch wenn das Problem sehr kompliziert erscheint
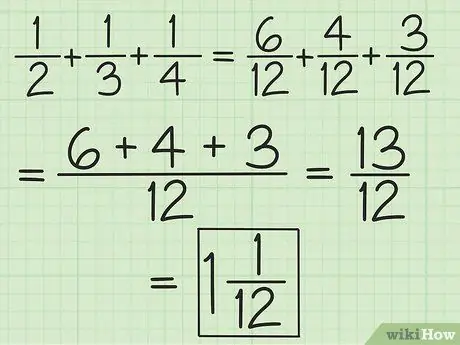
Schritt 2. Ordne die Nenner aller Brüche zu oder arbeite paarweise von links nach rechts, um mehr als zwei Brüche zu addieren und zu subtrahieren
Um beispielsweise 1/2, 1/3 und 1/4 zu addieren, können Sie sie in 6/12, 4/12 und 3/12 ändern, um 13/12 zu erhalten, oder Sie können 3/6 und 2. addieren /6, so dass Sie 5/6 erhalten, dann addieren Sie 5/6 und 1/4 (gleichen Sie die Nenner aus, sodass der zweite Bruch 3/12 wird), um 13/12 (10/12 plus 3/12) zu erhalten. Wandeln Sie es in eine gemischte Zahl um, die 1 1/12 ist
Tipps
- Denken Sie daran, dass Sie eine Menge Mathematik gelernt haben. Mathematik ist wie eine Sprache, die man fließend aussprechen kann, und nun versucht man, sie lesen und schreiben zu lernen.
- Denken Sie daran, das Endergebnis Ihrer Berechnung immer zu vereinfachen, egal ob Ihr Problem in Form eines gewöhnlichen Bruchs, einer gemischten Zahl oder eines komplexen Bruchs vorliegt.






