- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:12.
- Zuletzt bearbeitet 2025-01-23 12:14.
Einen Bruch durch einen Bruch zu teilen mag zunächst verwirrend erscheinen, ist aber eigentlich ganz einfach. Alles, was Sie tun müssen, ist umdrehen, multiplizieren und vereinfachen! Dieser Artikel führt Sie durch den Prozess und zeigt Ihnen, wie einfach es ist, einen Bruch durch einen Bruch zu teilen.
Schritt
Teil 1 von 2: Wie man Brüche durch Brüche teilt
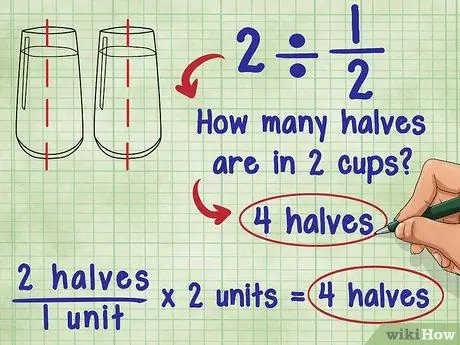
Schritt 1. Überlegen Sie, was das Teilen durch einen Bruch bedeutet
Über 2 ÷ 1/2 fragte Ada: "Wie viele Hälften sind in 2?" Die Antwort ist 4, weil jede Einheit (1) aus zwei „halben“besteht und es insgesamt 2 Einheiten gibt: 2 „halb“/1 Einheit * 2 Einheiten = 4 „halb“.
- Stellen Sie sich die gleiche Gleichung mit einem Glas Wasser vor: Wie viel und ein halbes Glas Wasser sind in 2 Gläsern Wasser? Sie können 2 ½ Tassen Wasser in jedes Glas Wasser gießen. Das heißt im Grunde addiert man die „halben“Gläser Wasser, und man hat zwei Gläser: 2 „halb“/1 Tasse * 2 Tassen = 4 „halb“.
- Das heißt, wenn der Bruch, den Sie teilen, zwischen 0 und 1 liegt, ist die Antwort immer größer als die ursprüngliche Zahl! Dies ist der Fall, wenn Sie eine ganze Zahl oder einen Bruch durch einen Bruch teilen.

Schritt 2. Verstehe, dass Dividieren das Gegenteil von Multiplizieren ist
Somit kann die Division durch einen Bruch gelöst werden, indem mit dem Kehrwert des Bruchs multipliziert wird. Der Kehrwert eines Bruchs (auch „Multiplikationsinverse“genannt) ist der Bruch, der invertiert wird, sodass Zähler und Nenner die Plätze tauschen. Gleich werden wir Brüche durch Brüche dividieren, indem wir den Kehrwert des zweiten Bruchs ermitteln und beide Brüche multiplizieren. Schauen wir uns jedoch zuerst einige der Gegensätze an:
- Der Kehrwert von 3/4 ist 4/3.
- Das Gegenteil von 7/5 ist 5/7.
- Der Kehrwert von 1/2 ist 2/1 oder 2.
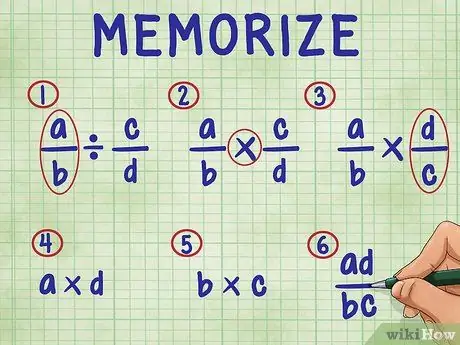
Schritt 3. Denken Sie an die folgenden Schritte, um einen Bruch durch einen Bruch zu dividieren
Die Schritte umfassen der Reihe nach:
- Lassen Sie einfach den ersten Bruch in der Gleichung.
- Ändern Sie das Divisionszeichen in das Multiplikationszeichen.
- Invertieren Sie den zweiten Bruch (bestimmen Sie seinen Kehrwert).
- Multipliziere den Zähler (obere Zahl) beider Brüche. Das Multiplikationsergebnis ist der Zähler (oben) Ihrer Antwort.
- Multipliziere den Nenner (untere Zahl) beider Brüche. Das Produkt des Produkts ist der Nenner Ihrer Antwort.
- Vereinfachen Sie Ihre Brüche, indem Sie sie auf ihre einfachsten Begriffe vereinfachen.
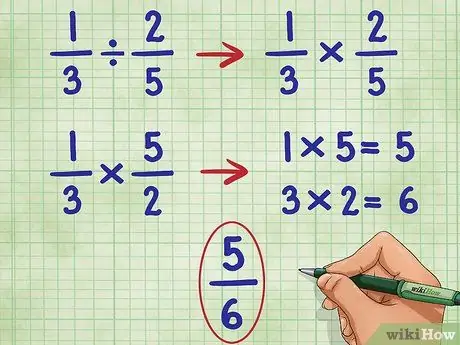
Schritt 4. Führen Sie diese Schritte für das Beispiel 1/3 2/5 aus
Wir beginnen damit, dass wir den ersten Bruch weglassen und das Divisionszeichen in das Multiplikationszeichen umwandeln:
- 1/3 ÷ 2/5 = Wird:
- 1/3 * _ =
- Nun kehren wir den zweiten Bruch (2/5) um, um seinen Kehrwert zu finden, der 5/2 ist:
- 1/3 * 5/2 =
- Multiplizieren Sie nun den Zähler (obere Zahl) beider Brüche, 1*5 = 5.
- 1/3 * 5/2 = 5/
- Multiplizieren Sie nun den Nenner (untere Zahl) beider Brüche, 3*2 = 6.
- Jetzt haben wir: 1/3 * 5/2 = 5/6
- Dieser Bruch lässt sich nicht weiter vereinfachen, also haben wir unsere Antwort.

Schritt 5. Versuchen Sie, sich die folgenden Reime zu merken, damit Sie sich besser erinnern können:
"Brüche zu teilen ist einfach, drehe den zweiten Bruch um und multipliziere dann. Vergiss nicht zu vereinfachen, bevor es Zeit zum Essen ist."
Eine weitere hilfreiche Erinnerungshilfe sagt Ihnen, was mit jedem Teil der Gleichung zu tun ist: „Lass mich (erster Bruch), mich ändern (Divisionszeichen), mich umkehren (zweiter Bruch).“
Teil 2 von 2: Brüche durch Brüche in Problemen dividieren
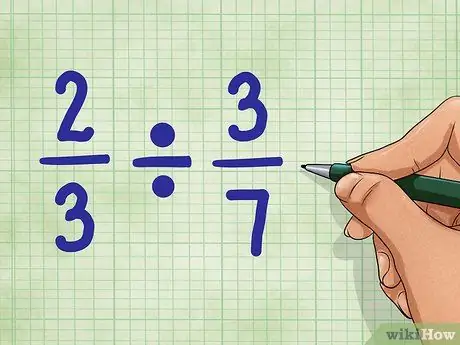
Schritt 1. Beginnen Sie mit Beispielfragen
Lass uns verwenden 2/3 ÷ 3/7. Diese Frage fragt nach der Anzahl der Teile gleich 3/7, die im Wert 2/3 zu finden ist. Mach dir keine Sorgen. Es ist nicht so schwer, wie es sich anhört!
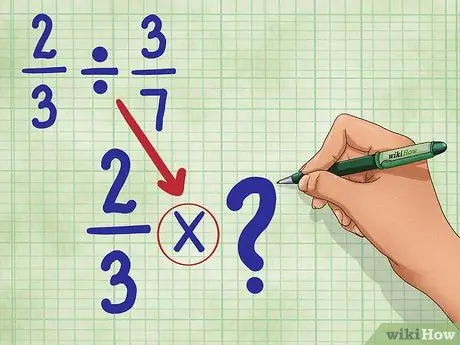
Schritt 2. Wandeln Sie das Divisionszeichen in das Multiplikationszeichen um
Ihre neue Gleichung lautet: 2/3 * _ (Wir werden diese Lücke gleich ausfüllen.)
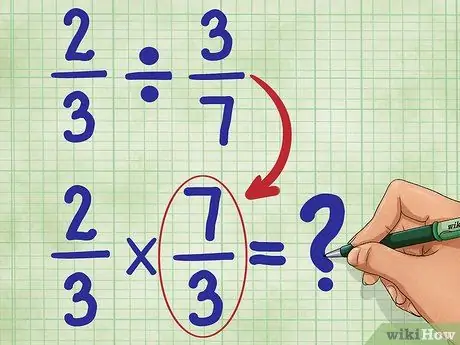
Schritt 3. Finden Sie nun den Kehrwert des zweiten Bruchs
Das bedeutet, 3/7 umzudrehen, so dass der Zähler (3) jetzt unten und der Nenner (7) jetzt oben ist. Der Kehrwert von 3/7 ist 7/3. Schreiben Sie nun Ihre neue Gleichung:
2/3 * 7/3 = _

Schritt 4. Multiplizieren Sie Ihre Brüche
Multipliziere zunächst die Zähler beider Brüche: 2 * 7 = 14. 14 ist der Zähler (oberste Zahl) Ihrer Antwort. Dann multiplizieren Sie die Nenner der beiden Brüche: 3 * 3 = 9. 9 ist der Nenner (untere Zahl) Ihrer Antwort. Das weißt du jetzt 2/3 * 7/3 = 14/9.
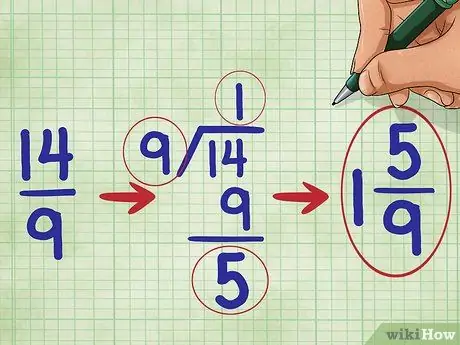
Schritt 5. Vereinfachen Sie Ihren Bruch
Da bei diesem Problem der Zähler des Bruchs größer als der Nenner ist, wissen wir, dass unser Bruch größer als 1 ist. Wir müssen ihn in eine gemischte Zahl umwandeln. (Eine gemischte Zahl ist eine ganze Zahl und ein Bruch kombiniert, zum Beispiel 1 2/3.))
-
Teilen Sie zuerst den Zähler
Schritt 14. mit 9.
Die Zahl 14 geteilt durch 9 ergibt eins mit einem Rest von 5. Sie sollten Ihren vereinfachten Bruch also wie folgt aufschreiben: 1 5/9 („eins fünfneuntel“).
- Stoppen Sie, Sie haben die Antwort gefunden! Sie können angeben, dass Sie den Bruch nicht mehr vereinfachen können, weil der Nenner nicht durch den Zähler teilbar ist (9 ist nicht durch 5 teilbar) und der Zähler eine Primzahl oder eine ganze Zahl ist, die nur durch eins und die Zahl selbst teilbar ist.
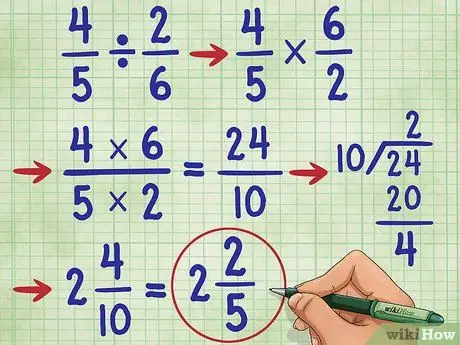
Schritt 6. Versuchen Sie ein anderes Beispiel
Versuchen wir es mit der Frage 4/5 ÷ 2/6 =. Ändern Sie zuerst das Divisionszeichen in das Multiplikationszeichen (4/5 * _ =), dann finde den Kehrwert von 2/6, also 6/2. Nun hast du die Gleichung: 4/5 * 6/2 =_. Multiplizieren Sie nun den Zähler, 4 * 6 = 24, und der Nenner 5* 2 = 10. Jetzt hast du 4/5 * 6/2 = 24/10.
Vereinfachen Sie nun den Bruch. Da der Zähler größer als der Nenner ist, müssen wir diesen Bruch in eine gemischte Zahl umwandeln.
- Teilen Sie zuerst den Zähler durch den Nenner (24/10 = 2 verbleibende 4).
- Schreiben Sie die Antwort als 2 4/10. Wir können diesen Bruch noch einmal vereinfachen!
- Beachten Sie, dass 4 und 10 gerade Zahlen sind. Der erste Schritt zur Vereinfachung besteht also darin, jede Zahl durch 2 zu teilen. Wir erhalten 2/5.
- Da der Nenner (5) nicht durch den Zähler (2) teilbar ist und 5 eine Primzahl ist, wissen wir, dass dieser Bruch nicht weiter vereinfacht werden kann. Unsere Antwort lautet also: 2 2/5.

Schritt 7. Holen Sie sich zusätzliche Hilfe beim Vereinfachen von Brüchen
Sie haben wahrscheinlich viel Zeit damit verbracht, zu lernen, wie man Brüche vereinfacht, bevor Sie versucht haben, sie durcheinander zu teilen. Wenn Sie jedoch eine Auffrischung oder andere Hilfe benötigen, gibt es einige großartige Online-Artikel, die Ihnen eine große Hilfe sein können.
Verwandte wikiHow-Artikel
- Konvertieren von gewöhnlichen Brüchen in Dezimalzahlen
- Berechnen der Fläche eines Kreises
- Dividieren von Polynomen durch synthetische Division
- Gemischte Brüche teilen






