- Autor Jason Gerald [email protected].
- Public 2023-12-16 11:03.
- Zuletzt bearbeitet 2025-01-23 12:15.
Das Zählen von Brüchen ist eine der nützlichsten mathematischen Fähigkeiten, die es zu entwickeln gilt. Bevor Sie Bruchrechnungen durchführen, erfahren Sie, wie Sie Teile und Typen von Brüchen identifizieren. Danach können Sie sie addieren oder subtrahieren. Für komplexere Berechnungen lernen Sie, wie man Brüche multipliziert und dividiert. Normalerweise müssen Sie auch Brüche vereinfachen oder reduzieren.
Schritt
Methode 1 von 4: Brüche erkennen

Schritt 1. Finden Sie den Bruch
Brüche werden als eine Zahl oberhalb der Trennlinie und eine weitere Zahl unterhalb der Linie geschrieben.
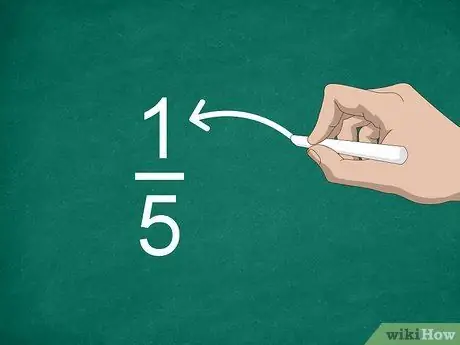
Schritt 2. Identifizieren Sie den Zähler
Die Zahl über der Linie wird als Zähler bezeichnet und zeigt an, wie viele Teile der Bruch hat.
Im Bruch 1/5 ist beispielsweise „1“der Zähler
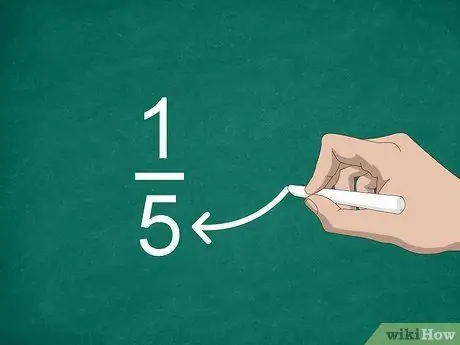
Schritt 3. Finden Sie den Nenner
Die Zahl unterhalb der Linie wird als Nenner bezeichnet. Dieser Wert gibt die Anzahl der Teile an, die eine ganze Zahl "konstruieren".
Im Bruch 1/5 ist beispielsweise "5" der Nenner, sodass der Bruch fünf Teile hat

Schritt 4. Bestimmen Sie, ob die Brüche vernünftige Brüche oder unechte Brüche sind
Ist der Zähler kleiner als der Nenner, ist der Bruch ein natürlicher Bruch. Bei unechten Brüchen ist der Zähler größer als der Nenner.
- 3/4 ist beispielsweise ein vernünftiger Bruch und 5/3 ein unechter Bruch.
- Wenn Sie eine ganze Zahl haben, die einen Bruch enthält, wird die Zahl als gemischte Zahl bezeichnet. 1 1/2 ist beispielsweise eine gemischte Zahl.
Methode 2 von 4: Brüche addieren oder subtrahieren

Schritt 1. Identifizieren Sie Brüche mit demselben Nenner
Wenn Sie Brüche addieren oder subtrahieren müssen, muss jeder Bruch den gleichen Nenner haben, bevor Sie die Berechnung durchführen. Beobachten Sie den Nenner jedes Bruchs, um sicherzustellen, dass sie alle gleich (ähnlich) sind.
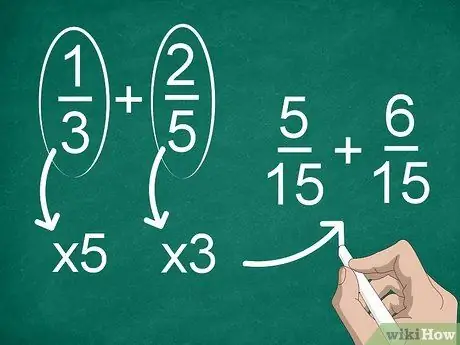
Schritt 2. Finden Sie einen gemeinsamen Nenner, wenn jeder Bruch einen anderen Nenner hat
Wenn die Nenner nicht gleich sind, müssen Sie die Brüche ändern, damit sie denselben Nenner haben. Um einen gemeinsamen Nenner zu finden, multiplizieren Sie jeden Bruch mit dem Nenner des anderen.
Um beispielsweise einen gemeinsamen Nenner in 1/3 + 2/5 zu finden, multiplizieren Sie „1“und „3“mit „5“, dann multiplizieren Sie „2“und „5“mit „3“. Jetzt haben Sie die Addition von 15.05. + 15.06. Danach können Sie die Brüche berechnen
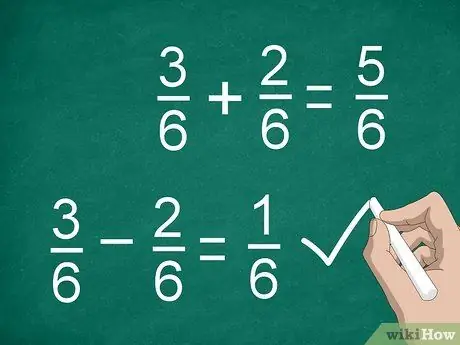
Schritt 3. Addieren oder subtrahieren Sie die Zähler, um Brüche zu berechnen
Sobald Sie einen gemeinsamen Nenner gefunden und die Zähler (falls erforderlich) multipliziert haben, können Sie addieren oder subtrahieren. Addiere oder subtrahiere die Zähler und platziere das Ergebnis über der Trennlinie. Schreibe den gemeinsamen Nenner unter die Linie.
- Zum Beispiel 3/6 - 2/6 = 1/6.
- Addieren oder subtrahieren Sie die Nenner nicht.
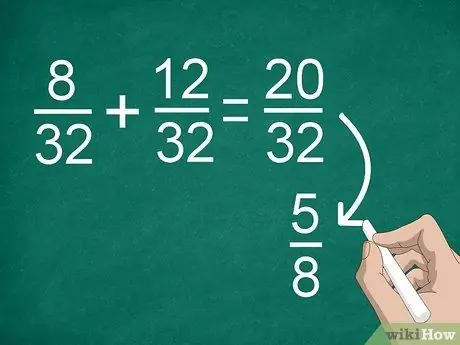
Schritt 4. Vereinfachen Sie die Ergebnisse, falls erforderlich
Wenn Sie zuvor einen gemeinsamen Nenner finden mussten, erhalten Sie möglicherweise einen großen Bruch, den Sie vereinfachen können. Wenn Sie beispielsweise 8/32 +12/32 hinzufügen, erhalten Sie als Ergebnis „20/32“. Dieser Bruch kann auf „5/8“vereinfacht werden.
Methode 3 von 4: Brüche multiplizieren und vereinfachen
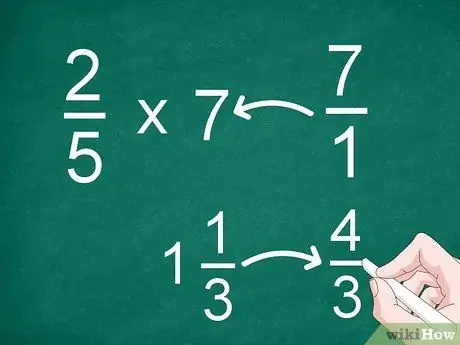
Schritt 1. Wandeln Sie gemischte Brüche oder ganze Zahlen in unechte Brüche um
Um die Multiplikation zu vereinfachen, müssen Sie jede Zahl in einen vernünftigen oder unechten Bruch umwandeln. Wenn Sie ganze Zahlen oder gemischte Zahlen haben, die multipliziert werden müssen, konvertieren Sie sie zuerst in einen gemeinsamen Bruch (natürlich oder unecht).
- Um beispielsweise 2/5 mit 7 zu multiplizieren, wandeln Sie "7" in einen Bruch um. Danach können Sie 2/5 mit 7/1 multiplizieren.
- Wenn Sie eine gemischte Zahl wie 1 1/3 haben, konvertieren Sie sie vor dem Multiplizieren in einen unechten Bruch („4/3“).
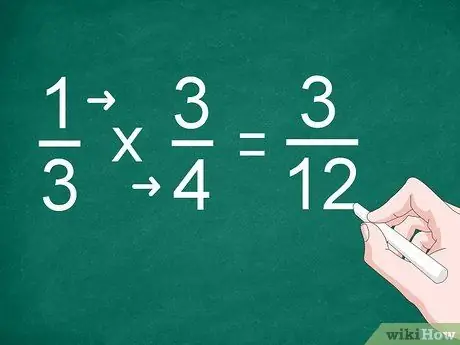
Schritt 2. Multiplizieren Sie jeden Zähler und Nenner
Anstatt zu addieren, multiplizieren Sie den Zähler und schreiben Sie das Ergebnis über die Trennlinie. Außerdem müssen Sie die Nenner multiplizieren und das Ergebnis unter die Linie schreiben.
Um beispielsweise 1/3 mit 3/4 zu multiplizieren, multiplizieren Sie „1“mit „3“, um den Zähler zu erhalten. Multiplizieren Sie „3“mit „4“, um den Nenner zu erhalten. Die Antwort auf die Multiplikation ist "3/12"

Schritt 3. Vereinfachen Sie die Ergebnisse
Normalerweise müssen Sie das Ergebnis auf eine einfachere Form reduzieren, insbesondere wenn Sie anfangs unnatürliche Brüche haben. Finden Sie den größten gemeinsamen Faktor und verwenden Sie diesen Faktor, um Zähler und Nenner zu vereinfachen.
Für den Bruch 3/12 beispielsweise ist der größte gemeinsame Faktor zwischen „3“und „12“„3“. Dividiere jedes Element des Bruchs durch „3“, bis du den Bruch „1/4“erhältst
Methode 4 von 4: Brüche dividieren
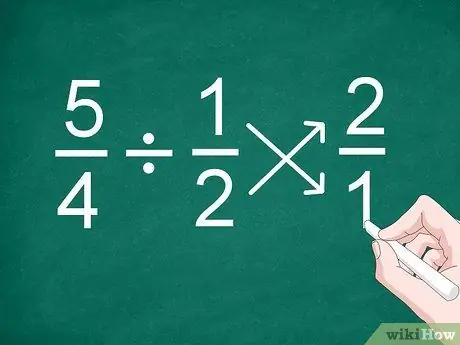
Schritt 1. Kehren Sie die Position des zweiten Bruchs um
Der einfachste Weg, Brüche zu teilen, sogar Brüche mit unterschiedlichen Nennern, besteht darin, die Position des zweiten Bruchs umzukehren, bevor Sie das Ergebnis berechnen.
Zum Beispiel für das Problem 5/4 1/2, kehren Sie die Position des Bruches „1/2“um, um „2/1“zu werden
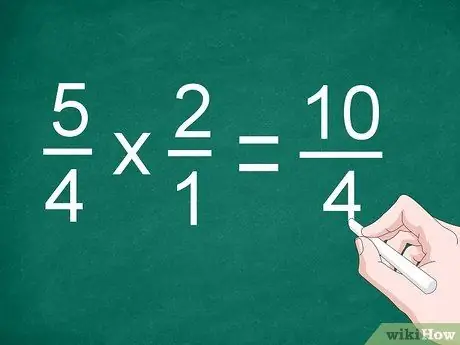
Schritt 2. Multiplizieren Sie Zähler und Nenner
Multipliziere Brüche direkt, um die Zähler zu multiplizieren. Schreiben Sie das Ergebnis über die Trennlinie und multiplizieren Sie dann den Nenner. Notieren Sie das Produkt der Nenner unter der Linie.
Multiplizieren Sie im vorherigen Beispiel 5/4 mit 2/1, um „10/4“zu erhalten
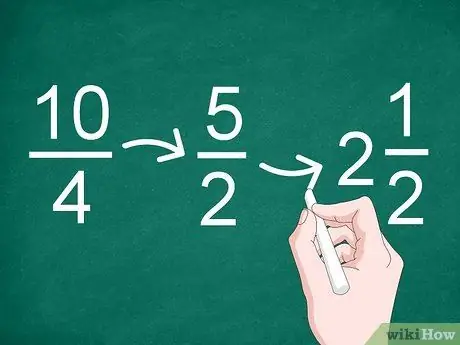
Schritt 3. Vereinfachen Sie die Ergebnisse, falls erforderlich
Wenn das Ergebnis der Division ein unechter Bruch ist oder gekürzt werden kann, vereinfachen Sie den Bruch. Verwenden Sie den größten gemeinsamen Faktor, um den Bruch zu reduzieren.
- Zum Beispiel ist der größte gemeinsame Faktor im Bruch 10/4 „2“, so dass das Ergebnis der Vereinfachung „5/2“ist (10 geteilt durch 2 und 4 geteilt durch 2).
- Da das Ergebnis der Vereinfachung ein unechter Bruch ist, können Sie ihn in eine ganze Zahl und einen Bruch (eine gemischte Zahl) umwandeln. Daher kann 5/2 in „2“geändert werden.
Tipps
- Wenn Sie mit komplexen Brüchen arbeiten, müssen Sie einige zusätzliche Schritte ausführen, um den Bruch zu vereinfachen. Diese Vereinfachung selbst ist jedoch zwingender Bestandteil des Berechnungsprozesses.
- Schreiben Sie Brüche immer sauber, um das Risiko von Fehleinschätzungen zu verringern.






