- Autor Jason Gerald [email protected].
- Public 2023-12-16 11:03.
- Zuletzt bearbeitet 2025-01-23 12:14.
Wenn Sie bereits verstanden haben, ist es nicht schwierig, gewöhnliche Brüche in Dezimalzahlen umzuwandeln. Um gewöhnliche Brüche in Dezimalzahlen umzuwandeln, können Sie lange Divisionen, Multiplikationen oder sogar einen Taschenrechner verwenden, wenn Sie nicht von Hand rechnen möchten. Sobald Sie die Methode beherrschen, können Sie Brüche problemlos in Dezimalzahlen umwandeln.
Schritt
Methode 1 von 4: Mit langer Division
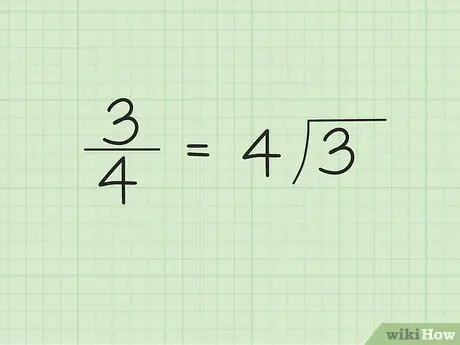
Schritt 1. Schreiben Sie den Nenner außerhalb/links des Divisorsymbols und den Zähler innerhalb/rechts des Divisorsymbols
Angenommen, wir möchten 3/4 in eine Dezimalzahl umwandeln. Schreiben Sie „4“außerhalb/linke Seite des Teilersymbols und „3“innerhalb/rechts Seite des Teilersymbols. „4“ist die Zahl, die dividiert und „3“ist die Zahl, die geteilt wird.

Schritt 2. Schreiben Sie „0“und dann einen Dezimalpunkt (ein Komma) über das Divisor-Symbol
Da es sich um einen Bruch handelt, muss das Ergebnis kleiner als eins sein, daher ist dieser Schritt sehr wichtig. Schreiben Sie danach das Dezimalzeichen, dann „0“, nach der Zahl „3“in/rechts vom Divisor-Symbol. Obwohl „3“gleich „3, 0“ist, erlaubt die Null, dass „3, 0“durch „4“geteilt wird.

Schritt 3. Berechnen Sie die Antwort mit langer Division
Bei der langen Division kann das Dezimalzeichen vorerst ignoriert werden, sodass Sie nur 30 dividiert durch 4 berechnen müssen. So geht's:
- Teilen Sie zuerst 3, 0, was als 30 zählt, durch 4. Die nächste 4 bis 30 ist 4 x 7 = 28, so dass 2 übrig bleibt. Schreiben Sie also „7“nach „0“, über den Teiler und „28“unter „ 3, 0” in/rechte Seite des Teilersymbols. Unter 28 schreiben Sie "2", den Rest von 30 minus 28.
- Als nächstes schreiben Sie „0“nach „3, 0“, so dass es „3, 00“wird, was als „300“betrachtet werden kann, innerhalb/rechter Seite des Teilersymbols. Somit kann 0 rechts von „2“abgesenkt werden, sodass „20“durch „4“teilbar ist.
- „20“geteilt durch „4“ergibt „5“. Schreiben Sie also "5" nach "0.7" über das Divisor-Symbol, so dass es "0.75" wird.

Schritt 4. Schreiben Sie die endgültige Antwort
„3“geteilt durch „4“ergibt also „0,75“. Schreiben Sie die Antwort auf. Fertig.
Methode 2 von 4: Brüche, die sich wiederholende Dezimalstellen erzeugen
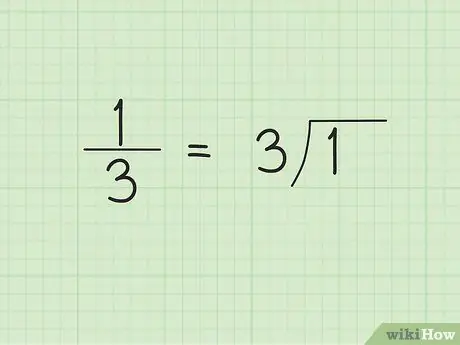
Schritt 1. Machen Sie eine lange Division
Wenn Sie mit der Division von langen Ziffern beginnen, können Sie möglicherweise nicht vorhersagen, dass das Ergebnis eine sich wiederholende Dezimalzahl ist. Nehmen wir zum Beispiel an, wir möchten den gewöhnlichen Bruch 1/3 in die Dezimalform umwandeln. Schreiben Sie 3 oder den Nenner auf die äußere/linke Seite des Teilersymbols und 1 innerhalb/rechte Seite des Teilersymbols.

Schritt 2. Schreiben Sie eine 0 und dann ein Dezimalzeichen über das Divisorsymbol
Da das Ergebnis kleiner als 1 sein muss, wird in diesem Schritt die Antwort in Dezimalform geschrieben. Das Dezimalzeichen muss auch rechts von der Zahl „1“geschrieben werden, die sich im/rechts vom Teilersymbol befindet.
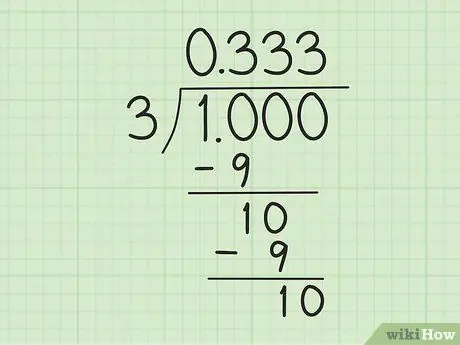
Schritt 3. Beginnen Sie mit der Berechnung der Division der langen Division
Beginnen Sie damit, aus „1“eine „1,0“zu machen, die als „10“zählt, sodass sie durch „3“teilbar ist. Führen Sie als nächstes die folgenden Schritte aus:
- Teilen Sie 10 durch 3. Verwenden Sie 3 x 3 = 9, um einen Rest von 1 zu bilden. Schreiben Sie also 3 rechts von der „0“über das Divisor-Symbol und subtrahieren Sie 10 durch 9, um den Rest von 1 zu erhalten.
- Schreiben Sie eine „0“rechts neben die Zahl „1“(der Rest von 10 minus 9 im vorherigen Schritt), um eine weitere „10“zu erhalten. Beim erneuten Dividieren von „10“durch „3“wird der gleiche Vorgang wiederholt: „3“rechts neben der ersten „3“über dem Divisor-Symbol schreiben und die neue „10“durch „9“subtrahieren.
- Fahren Sie fort, bis ein Muster entsteht. Weißt du, dass etwas seltsam ist? Diese Teilung kann ewig so weitergehen. 10 ist immer durch 3 teilbar: Es wird immer eine „1“unten und eine neue „3“nach dem Komma über dem Teilersymbol geben.
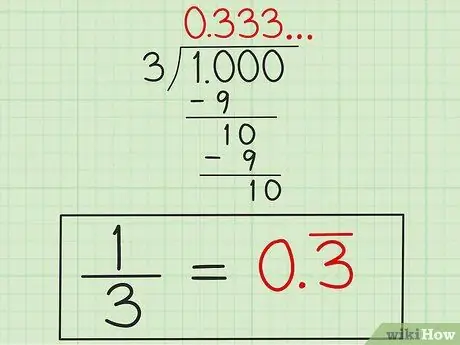
Schritt 4. Schreiben Sie die Antwort
Nachdem Sie wissen, dass sich "3" wiederholen wird, schreiben Sie die Antwort als "0, 3" mit einer Linie über der Zahl "3" (oder "0, 33" mit einer Linie über beiden Zahlen "3") als Hinweis darauf, dass die Nummer "3" wiederholt es sich immer wieder. Diese Antwort ist in der Dezimalform 1/3, da 1 geteilt durch 3 nicht von selbst endet.
Es gibt viele Brüche, die sich wiederholende Dezimalzahlen erzeugen, wie 2/9 („0, 2“mit „2“Wiederholung), 5/6 („0, 83“mit „3“Wiederholung) oder 7/9 („0, 7“mit „7“wiederholt sich). Dieses Muster tritt immer dann auf, wenn der Nenner ein Vielfaches von 3 ist und der Zähler nicht durch den Nenner teilbar ist
Methode 3 von 4: Durch Multiplikation

Schritt 1. Finden Sie die Zahl, die mit dem Nenner des Bruchs multipliziert werden kann, um 10, 100, 1.000 oder eine beliebige Zahl zur Basis 10 zu erhalten
Dies kann eine einfache Möglichkeit sein, Brüche in Dezimalzahlen umzuwandeln, ohne eine lange Division oder einen Taschenrechner zu verwenden. Suchen Sie zunächst eine Zahl, die mit dem Nenner des Bruchs multipliziert werden kann, um 10, 100, 1.000 usw. zu erhalten. Teilen Sie dazu zuerst 10, dann 100, dann 1.000 usw. durch den Nenner, bis Sie eine ganze Zahl erhalten. Beispiel:
- 3/5. 10/5 = 2,2 ist eine ganze Zahl. 2 kann mit 5 multipliziert werden, um 10 zu ergeben. Also kann 2 verwendet werden.
- 3/4. 10/4 = 2, 5. 2, 5 ist keine ganze Zahl. 100/4 = 25. 25 ist eine ganze Zahl. 25 kann mit 4 multipliziert werden, um 100 zu ergeben. Also kann 25 verwendet werden.
- 5/16. 10/16 = 0, 625, 100/16 = 6, 25, 1.000/16 = 62, 5, 10.000/16 = 625. 625 ist die erste erhaltene ganze Zahl. 625 kann mit 16 multipliziert werden, um 10.000 zu erhalten. Es kann also 625 verwendet werden.
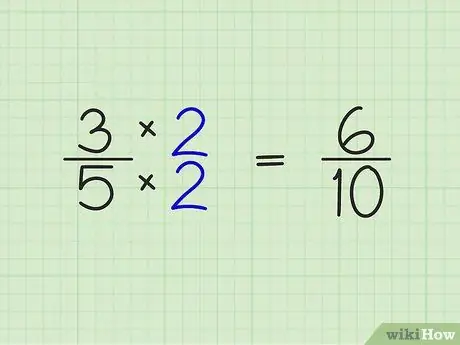
Schritt 2. Multiplizieren Sie Zähler und Nenner des Bruchs mit der ganzen Zahl aus dem vorherigen Schritt
Dieser Schritt ist ganz einfach. Multiplizieren Sie einfach die Zahlen über und unter dem Bruch mit der ganzen Zahl, die Sie im vorherigen Schritt erhalten haben. Beispiel:
- 3/5 x 2/2 = 6/10
- 3/4 x 25/25 = 75/100
- 5/16 x 625/625 = 3,125/10000

Schritt 3. Schreiben Sie die endgültige Antwort
Die Antwort ist, dass der Zähler mit einer Dezimalzahl entsprechend der Anzahl der Nullen im Nenner gekennzeichnet ist. Zählen Sie einfach, wie viele Nullen im Nenner sind. Wenn der Nenner nur 1 0 enthält, verschieben Sie den Dezimalpunkt um 1 Stelle nach links usw. Beispiel:
- 3/5 = 6/10 = 0, 6
- 3/4 = 75/100 = 0, 75
- 5/16 = 3.125/10.000 = 0, 3125
Methode 4 von 4: Mit Rechner

Schritt 1. Teilen Sie den Zähler durch den Nenner
Diese Methode ist sehr einfach. Verwenden Sie einfach einen Taschenrechner, um den Zähler, die Zahl am oberen Ende des Bruchs, durch den Nenner, die Zahl am unteren Ende des Bruchs, zu dividieren. Angenommen, Sie möchten 3/4 in eine Dezimalzahl umwandeln. Drücken Sie einfach "3", dann das Divisionssymbol ("÷'"), dann "4" und schließlich das Gleichheitssymbol ("=").

Schritt 2. Schreiben Sie die Antworten auf, die Sie erhalten
Die Antwort ist 0,75. Die dezimale Form des gemeinsamen Bruchs 3/4 ist also 0,75.
Tipps
- Um zu überprüfen, ob Ihre Antwort richtig ist, multiplizieren Sie die Antwort mit dem Nenner des Bruchs. Wenn Ihre Antwort richtig ist, ist das Produkt der Multiplikation der Zähler des Bruchs.
- Einige Brüche können in Dezimalzahlen umgewandelt werden, indem vergleichbare Brüche erstellt werden, deren Nenner die Basis 10 (10, 100, 1.000 usw.) sind. Als nächstes verwenden Sie Stellenwerte, um die richtige Dezimalform aufzuschreiben.






