Brüche durch ganze Zahlen zu dividieren ist nicht so schwierig, wie es scheint. Um einen Bruch durch eine ganze Zahl zu dividieren, musst du nur die ganze Zahl in einen Bruch umwandeln, den Kehrwert des Bruchs ermitteln und das Ergebnis mit dem ersten Bruch multiplizieren. Wenn Sie wissen möchten, wie es geht, folgen Sie einfach diesen Schritten:
Schritt
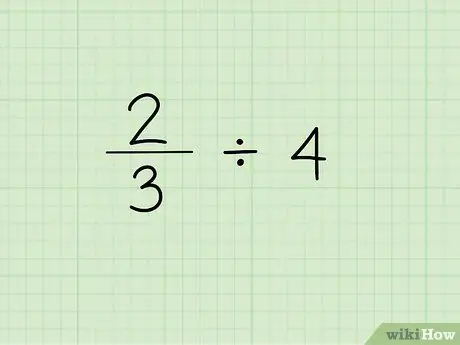
Schritt 1. Schreiben Sie das Problem auf
Der erste Schritt zum Dividieren eines Bruchs durch eine ganze Zahl besteht darin, den Bruch gefolgt vom Teilungszeichen und der ganzen Zahl zu schreiben, die Sie zum Teilen des Bruchs benötigen. Nehmen wir an, wir arbeiten mit folgendem Problem: 2/3 4.
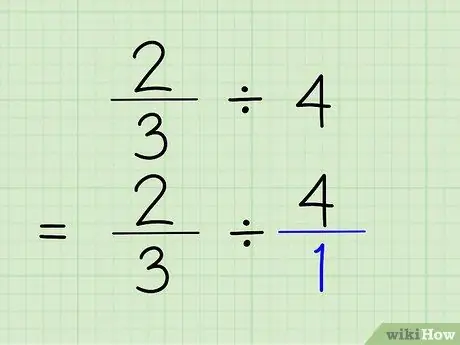
Schritt 2. Konvertieren Sie ganze Zahlen in Brüche
Um eine ganze Zahl in einen Bruch umzuwandeln, musst du nur die ganze Zahl über der Zahl 1 platzieren. Die ganze Zahl wird zum Zähler und 1 zum Nenner des Bruchs. 4/1 zu sagen ist wirklich dasselbe wie 4 zu sagen, weil Sie nur zeigen, dass die Zahl viermal "1" enthält. Das Problem wird 2/3 4/1 sein.
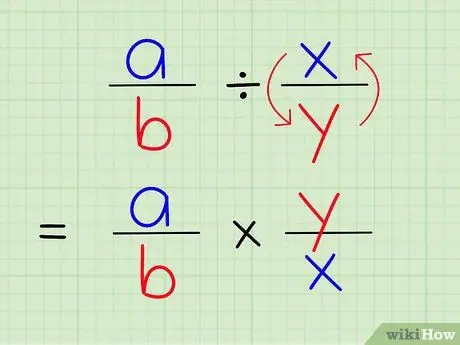
Schritt 3. Einen Bruch durch einen anderen zu dividieren ist dasselbe, wie diesen Bruch mit dem Kehrwert eines anderen Bruchs zu multiplizieren
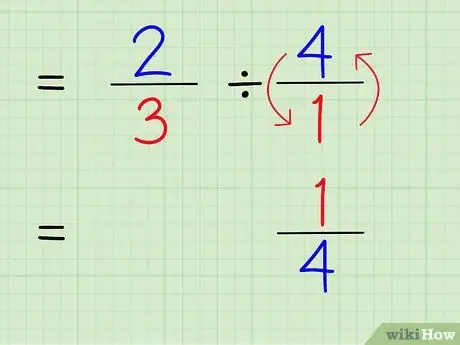
Schritt 4. Schreiben Sie den Kehrwert der ganzen Zahl
Um den Kehrwert einer Zahl zu ermitteln, vertauschen Sie Zähler und Nenner der Zahl. Um den Kehrwert von 4/1 zu finden, vertauschen Sie daher einfach den Zähler und den Nenner, so dass die Zahl 1/4 wird.
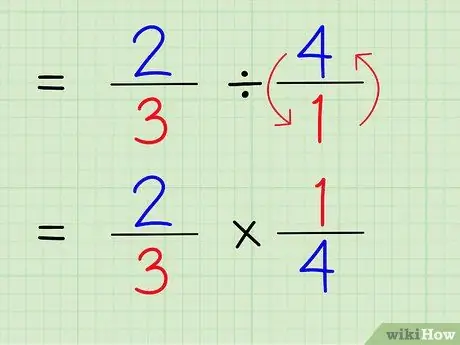
Schritt 5. Ändern Sie das Divisionszeichen in das Multiplikationszeichen
Das Problem wird 2/3 x 1/4 sein.
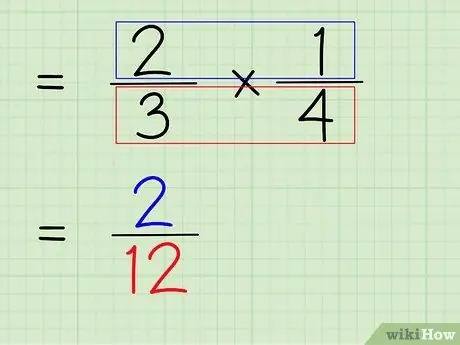
Schritt 6. Multiplizieren Sie Zähler und Nenner des Bruchs
Der nächste Schritt besteht also darin, Zähler und Nenner des Bruchs zu multiplizieren, um einen neuen Zähler und Nenner als endgültige Antwort zu erhalten.
- Um die Zähler zu multiplizieren, multiplizieren Sie einfach 2 x 1, um 2 zu erhalten.
- Um die Nenner zu multiplizieren, multiplizieren Sie einfach 3 x 4, um 12 zu erhalten.
- 2/3 x 1/4 = 2/12
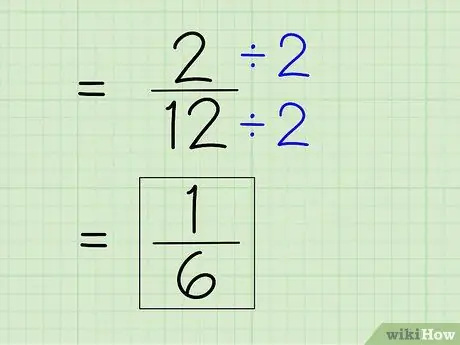
Schritt 7. Vereinfachen Sie den Bruch
Um einen Bruch zu vereinfachen, müssen Sie den kleinsten Nenner finden, dh Sie müssen Zähler und Nenner durch eine beliebige Zahl teilen, die beide Zahlen teilt. Da 2 der Zähler ist, müssen Sie sehen, ob 2 12 vollständig teilen kann – denn 12 ist eine gerade Zahl. Dann teilen Sie Zähler und Nenner durch 2, um einen neuen Zähler und Nenner zu erhalten, um eine einfache Antwort zu erhalten.
- 2 ÷ 2 = 1
- 12 ÷ 2 = 6
- Der Bruch 2/12 kann zu 1/6 vereinfacht werden. Dies ist Ihre letzte Antwort.
Tipps
- Dies dient der Gedächtnisunterstützung, eine einfache Möglichkeit, sich an all diese Berechnungen zu erinnern. Denken Sie daran: "Es ist einfach, Brüche zu teilen, die zweite Zahl umzukehren und zu multiplizieren!"
- Eine andere Variante der obigen Methode ist JGB/JBG. Ändern Sie nicht die erste Zahl. Wechseln Sie zur Multiplikation. Kehren Sie die letzte Zahl um. Oder zuerst B, dann G.
- Wenn Sie die Berechnung abbrechen, bevor Sie sie multiplizieren, müssen Sie möglicherweise nicht die einfachste Form des Bruchs finden, da das Ergebnis, wie Sie sehen können, bereits in der einfachsten Bruchform vorliegt. In unserem Beispiel können wir, bevor wir 2/3 × 1/4 multiplizieren, sehen, dass der erste Zähler (2) und der zweite Nenner (4) denselben Multiplikator von 2 haben, den wir löschen können, bevor wir mit der Berechnung fortfahren. Dies wandelt das Problem in 1/3 × 1/2 um, was ein sofortiges Ergebnis von 1/6 ergibt und uns Zeit spart, den Bruch zu einem späteren Zeitpunkt zu vereinfachen.
- Wenn einer Ihrer Brüche negativ ist, ist diese Methode immer noch praktikabel; Stellen Sie sicher, dass Sie die Schilder im Auge behalten, während Sie diese Schritte ausführen.
