- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:12.
- Zuletzt bearbeitet 2025-06-01 06:05.
Das Dividieren durch Dezimalzahlen scheint zunächst schwierig zu sein, da Ihnen niemand die „0,7-fache Tabelle“beigebracht hat. Das Geheimnis dabei ist, das Divisionsproblem in ein Format umzuwandeln, das nur ganze Zahlen verwendet. Nachdem Sie das Problem auf diese Weise umgeschrieben haben, wird es zu einem normalen langen Divisionsproblem.
Schritt
Teil 1 von 2: Schreibprobleme als gewöhnliche Divisionsprobleme
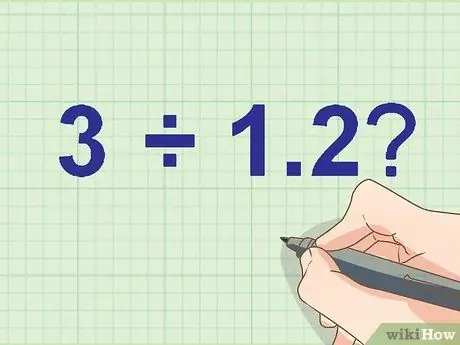
Schritt 1. Schreiben Sie Ihr Divisionsproblem auf
Verwenden Sie einen Bleistift, wenn Sie Ihre Arbeit verbessern möchten.
-
Beispiel:
Wie viele 3 ÷ 1, 2?

Schritt 2. Schreiben Sie die ganze Zahl als Dezimalzahl
Schreiben Sie einen Dezimalpunkt nach der ganzen Zahl und dann eine Null nach dem Dezimalpunkt. Tun Sie dies, bis beide Zahlen den gleichen Stellenwert rechts vom Komma haben. Der ganzzahlige Wert wird dadurch nicht geändert.
-
Beispiel:
In der Aufgabe 3 1, 2 ist unsere ganze Zahl 3. Da 1, 2 einen Stellenwert rechts vom Komma hat, schreiben Sie 3 als 3, 0, damit diese Zahl auch einen Stellenwert nach dem Komma hat. Jetzt wird unsere Angelegenheit 3, 0 ÷ 1, 2.
- Achtung: Keine Nullen links vom Dezimalpunkt hinzufügen! Die Zahl 3 ist gleich 3, 0 oder 3, 00, aber nicht gleich 30 oder 300.

Schritt 3. Verschieben Sie den Dezimalpunkt nach rechts, bis Sie eine ganze Zahl erhalten
Bei Divisionsproblemen können Sie die Dezimalpunkte verschieben, aber nur, wenn Sie die Dezimalpunkte aller Zahlen um die gleiche Anzahl von Schritten verschieben. Auf diese Weise können Sie das Problem in eine ganze Zahl umwandeln.
-
Beispiel:
Um 3, 0 1, 2 in eine ganze Zahl umzuwandeln, verschieben Sie den Dezimalpunkt um einen Schritt nach rechts. Somit wird aus 3, 0 30 und aus 1, 2 wird 12. Nun wird unser Problem 30 ÷ 12.

Schritt 4. Schreiben Sie das Problem mit langer Division
Platziere die teilbare Zahl (normalerweise die größere Zahl) unter dem langen Divisionssymbol. Schreiben Sie die Teilerzahl außerhalb dieses Symbols. Nun haben Sie ein reguläres Problem mit der langen Division, das ganze Zahlen verwendet. Wenn Sie sich daran erinnern möchten, wie man lange Divisionen durchführt, lesen Sie den nächsten Abschnitt.
Teil 2 von 2: Lösen von Problemen mit der langen Division

Schritt 1. Finden Sie die erste Ziffer der Antwort
Beginnen Sie mit der Lösung dieses Problems wie gewohnt, indem Sie den Teiler und die erste Ziffer der geteilten Zahl vergleichen. Berechnen Sie das Ergebnis der Division dieser ersten Ziffer durch die Zahl des Divisors und schreiben Sie dann das Ergebnis über diese Ziffer.
Beispiel: Wir versuchen, 30 durch 12 zu teilen. Vergleichen Sie 12 mit der ersten Ziffer der geteilten Zahl, die 3 ist. Da 12 größer als 3 ist, ist 3 geteilt durch 12 gleich 0. Schreiben Sie auf 0 über 3 in der Antwortzeile.
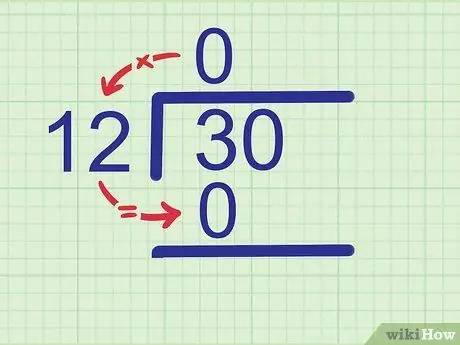
Schritt 2. Multiplizieren Sie den Quotienten mit dem Divisor
Schreiben Sie das Produkt des Produkts unter die Zahl, die geteilt wird. Schreiben Sie das Ergebnis direkt unter die erste Ziffer der Zahl, die Sie geteilt haben, denn dies ist die Ziffer, die Sie gerade gesehen haben.
-
Beispiel:
Da 0 x 12 = 0, schreibe 0 unter 3.
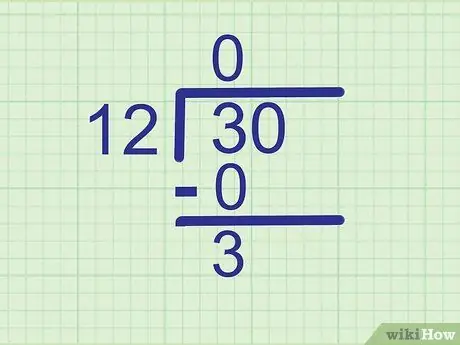
Schritt 3. Subtrahiere, um den Rest zu finden
Ziehen Sie das soeben berechnete Produkt von der direkt darüber liegenden Ziffer ab. Schreiben Sie die Antwort in eine neue Zeile darunter.
-
Beispiel:
3 - 0 = 3, also schreibe
Schritt 3. knapp unter 0.
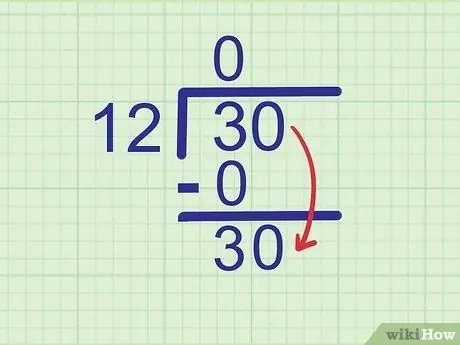
Schritt 4. Senken Sie die nächste Ziffer
Lassen Sie die nächste Ziffer der geteilten Zahl neben der gerade aufgeschriebenen Zahl fallen.
-
Beispiel:
Die geteilte Zahl ist 30. Wir haben die Zahl 3 gesehen, also ist die nächste Ziffer, die verringert werden muss, 0. Verkleinern Sie die Zahl 0 auf die Seite von 3, so dass sie zu wird
Schritt 30..
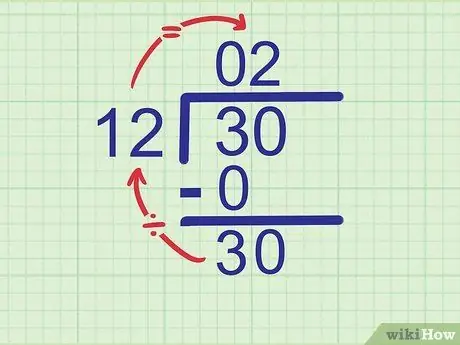
Schritt 5. Versuchen Sie, die neue Zahl durch den Divisor zu teilen
Wiederholen Sie nun den ersten Schritt in diesem Abschnitt, um die zweite Ziffer Ihrer Antwort zu finden. Vergleichen Sie dieses Mal den Divisor mit der Zahl, die Sie gerade in die untere Reihe geschrieben haben.
-
Beispiel:
Was ist der Quotient von 30 zu 12? Die nächste Antwort, die wir erhalten können, ist 2, weil 12 x 2 = 24. Schreiben Sie
Schritt 2. an zweiter Stelle der Antwortzeile.
- Wenn Sie sich bei der Antwort nicht sicher sind, versuchen Sie mehrere Multiplikationen, bis Sie die größte passende Antwort gefunden haben. Wenn Ihre Schätzung beispielsweise 3 ist, berechnen Sie 12 x 3 und Sie erhalten 36. Diese Zahl ist zu groß, weil wir versuchen, 30 zu berechnen. Versuchen Sie, eine Zahl zu verringern, 12 x 2 = 24. Diese Zahl passt. 2 ist also die richtige Antwort.

Schritt 6. Wiederholen Sie die obigen Schritte, um die nächste Nummer zu finden
Dies ist der gleiche lange Divisionsprozess wie oben und für jedes lange Divisionsproblem:
- Multiplizieren Sie die neue Ziffer Ihrer Antwort mit dem Divisor: 2 x 12 = 24.
- Schreiben Sie das Produkt in eine neue Zeile unterhalb der geteilten Zahl: Schreiben Sie 24 knapp unter 30.
- Ziehe die untere Reihe von der darüberliegenden Reihe ab: 30 - 24 = 6. Schreibe also 6 in eine neue Reihe darunter.

Schritt 7. Fahren Sie mit diesem Vorgang fort, bis Sie die letzte Antwortzeile abgeschlossen haben
Wenn die geteilte Zahl noch Ziffern enthält, verringern Sie die Ziffern und fahren Sie mit der Lösung des Problems auf die gleiche Weise fort. Wenn Sie die letzte Zeile mit Antworten ausgefüllt haben, fahren Sie mit dem nächsten Schritt fort.
-
Beispiel:
Wir haben gerade geschrieben
Schritt 2. in der letzten Antwortzeile. Fahren Sie mit dem nächsten Schritt fort.

Schritt 8. Fügen Sie Dezimalstellen hinzu, um die geteilte Zahl bei Bedarf zu „erweitern“
Wenn die Zahl gerade teilbar ist, ist Ihr endgültiges Subtraktionsergebnis „0“. Das heißt, Sie haben die Division beendet und erhalten eine Antwort in Form einer ganzen Zahl. Wenn Sie jedoch die letzte Antwortzeile ausgefüllt haben und noch Ziffern vorhanden sind, die geteilt werden können, müssen Sie die teilbare Zahl „erweitern“, indem Sie einen Dezimalpunkt gefolgt von der Zahl 0 hinzufügen. Denken Sie daran, dass dies nicht der Fall ist den Wert der Zahl nicht ändern.
-
Beispiel:
Wir sind bei der letzten Antwortzeile angelangt, aber die Antwort auf unsere letzte Subtraktion ist "6". Schreiben Sie „6, 0“unter das lange Divisionssymbol, indem Sie „, 0“zur letzten Ziffer hinzufügen. Schreiben Sie auch den Dezimalpunkt an der gleichen Stelle auf die Antwortzeile, aber schreiben Sie danach nichts mehr.

Schritt 9. Wiederholen Sie die gleichen Schritte, um die nächste Ziffer zu finden
Der einzige Unterschied besteht darin, dass Sie den Dezimalpunkt an der gleichen Stelle der Antwortzeile hinzufügen müssen. Sobald Sie dies getan haben, können Sie auf die gleiche Weise nach den verbleibenden Antwortziffern suchen.
-
Beispiel:
Lassen Sie die neue 0 bis zur letzten Zeile fallen, sodass sie „60“wird. Da 60 geteilt durch 12 genau 5 ist, schreibe
Schritt 5. als letzte Ziffer unserer Antwortzeile. Vergessen Sie nicht, dass wir eine Dezimalzahl in unsere Antwortzeile eingeben. So, 2, 5 ist die endgültige Antwort auf unsere Frage.
Tipps
- Sie können dies als Rest schreiben (also die Antwort auf 3 1, 2 ist „2 übrig 6“). Da Sie jedoch mit Dezimalzahlen arbeiten, erwartet Ihr Lehrer möglicherweise, dass Sie am Dezimalteil der Antwort arbeiten.
- Wenn Sie die lange Divisionsmethode richtig anwenden, haben Sie immer einen Dezimalpunkt an der richtigen Stelle oder gar keinen Dezimalpunkt, wenn die Zahl durch teilbar ist. Versuchen Sie nicht, die Nachkommastellen zu erraten. Die Nachkommastelle unterscheidet sich oft von der Nachkommastelle in Ihrer Startnummer.
- Wenn das Problem der langen Division nicht lange anhält, können Sie anhalten und auf die nächste Zahl runden. Um zum Beispiel 17 4, 2 zu lösen, zählen Sie einfach bis 4.047… und runden Sie Ihre Antwort auf „ungefähr 4.05“.
-
Denken Sie an Ihre Divisionsbedingungen:
- Die zu teilende Zahl ist die zu teilende Zahl.
- Der Divisor ist die Zahl, die zum Dividieren verwendet wird.
- Der Quotient ist die Antwort auf das mathematische Divisionsproblem.
- Ganzes: geteilt durch Divisor = Quotient.
Warnung
Denken Sie daran, dass 30 12 die gleiche Antwort wie 3 1, 2 ergibt. Versuchen Sie nicht, Ihre Antwort zu „korrigieren“, nachdem Sie die Dezimalstelle rückwärts verschoben haben
Verwandte wikiHow-Artikel
- Konvertieren von gewöhnlichen Brüchen in Dezimalzahlen
- Eine seit langem festgelegte Teilung durchführen
- Teile Brüche durch Brüche
- Gemischte Brüche teilen






