Um Brüche zu multiplizieren, musst du nur Zähler und Nenner multiplizieren und das Ergebnis vereinfachen. Um Brüche zu dividieren, musst du nur Zähler und Nenner eines Bruchs umkehren, das Ergebnis mit einem anderen multiplizieren und vereinfachen. Wenn Sie wissen möchten, wie man Brüche schnell teilt und multipliziert, befolgen Sie diese Schritte.
Schritt
Methode 1 von 2: Brüche multiplizieren
Schritt 1. Multiplizieren Sie den Zähler des Bruchs
Der Zähler ist die oberste Zahl des Bruchs und der Nenner die unterste Zahl des Bruchs. Der erste Schritt beim Multiplizieren von Brüchen besteht darin, die Brüche so auszurichten, dass Zähler und Nenner nebeneinander liegen. Wenn Sie den Bruch 1/2 mit 12/48 multiplizieren, müssen Sie als erstes die Zähler 1 und 12 multiplizieren. 1 x 12 = 12. Schreiben Sie das Produkt 12 in den Zähler Ihrer Antwort.
Schritt 2. Multiplizieren Sie den Nenner des Bruchs
Jetzt müssen Sie nur noch das gleiche wie beim Zähler machen. Multiplizieren Sie 2 und 48, um den neuen Nenner zu finden. 2 x 48 = 96. Schreiben Sie diese Antwort in den Nenner Ihrer Antwort. Somit ist der neue Bruch 12/96.
Schritt 3. Vereinfachen Sie den Bruch
Der letzte Schritt besteht darin, das Ergebnis zu vereinfachen, wenn Sie können. Um einen Bruch zu vereinfachen, musst du den größten gemeinsamen Faktor (GCF) von Zähler und Nenner finden. Der GCF ist die größte Zahl, die die beiden Zahlen teilen kann. In den Aufgaben 12 und 96 kommt es vor, dass 12 96 teilen kann. Teilen Sie also 12 durch 12, um 1 zu erhalten, und teilen Sie 96 durch 12, um 8 zu erhalten. Somit ist 12/96 12/12 = 1/8.
Wenn beide Zahlen gerade Zahlen sind, können Sie auch mit der Division durch 2 beginnen und die Division durch 2 fortsetzen. 12/96 2/2 = 6/48 2/2 = 3/24. Dann werden Sie feststellen, dass 24 durch 3 teilbar ist. Sie können also sowohl den Zähler als auch den Nenner durch 3 teilen, um 1/8 zu erhalten. 3/24 3/3 = 1/8
Methode 2 von 2: Brüche dividieren
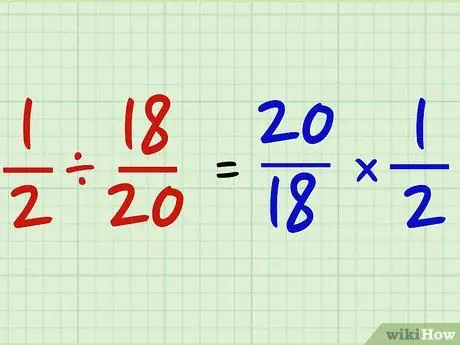
Schritt 1. Kehren Sie Nenner und Zähler eines der Brüche um und wandeln Sie das Divisionszeichen in eine Multiplikation um
Zum Beispiel teilen Sie 1/2 durch 18/20. Drehen Sie nun den Zähler von 18/20 auf 20/18 und wandeln Sie das Divisionszeichen in eine Multiplikation um. Also 1/2 18/20 = 1/2 x 20/18.
Schritt 2. Multiplizieren Sie Zähler und Nenner des Bruchs und vereinfachen Sie Ihre Antwort
Machen Sie jetzt dasselbe wie beim Multiplizieren von Brüchen. Wenn Sie die Zähler 1 und 20 multiplizieren, ist das Ergebnis 20 im Zähler. Wenn Sie die Nenner 2 und 18 multiplizieren, erhalten Sie 36 im Nenner. Das Ergebnis der Multiplikation von Brüchen ist 20/36. 4 ist die größte Zahl, die Zähler und Nenner dieses Bruchs teilen kann. Teilen Sie also beide durch 4, um die Antwort zu vereinfachen. 20/36 4/4 = 5/9.
Tipps
- Überprüfen Sie Ihre Arbeit.
- Denken Sie daran: Ganze Zahlen können als Bruch geschrieben werden: 2 entspricht 2/1.
- Vergessen Sie nie, zu vereinfachen.
- Cross-Doodle kann jederzeit verwendet werden, um Zeit zu sparen und gleichzeitig zu vereinfachen. Durchstreichen wird durch den gleichen Faktor diagonal geteilt. Beispielsweise kann die Frage (8/20)*(6/12) durchgestrichen werden als (2/10)*(3/3).
Warnung
- Mach es Schritt für Schritt. Dadurch wird die Möglichkeit des Auftretens von Fehlern verringert.
- Denken Sie daran, Brüche auf ihre einfachste Form zu vereinfachen. Eine nicht einfache Vereinfachung ist dasselbe wie keine Vereinfachung.
- Es gibt immer mehr als einen Weg, Dinge in der Mathematik zu erledigen. Aber nur weil Ihre Antwort richtig ist, wenn Sie ein Problem auf andere Weise lösen, heißt das nicht, dass es immer der richtige Weg ist. Eine andere Möglichkeit, Brüche zu teilen, ist zum Beispiel das Kreuzprodukt, das die Diagonalen multipliziert.
