- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:03.
- Zuletzt bearbeitet 2025-01-23 12:15.
Das Multiplizieren von Längen kann ein wenig entmutigend erscheinen, insbesondere wenn Sie zwei ziemlich große Zahlen multiplizieren. Wenn Sie dies jedoch Schritt für Schritt tun, können Sie lange Multiplikationen schnell durchführen. Machen Sie sich bereit, diese Mathe-Quiz zu lösen, indem Sie Schritt 1 unten sehen, um loszulegen.
Schritt
Methode 1 von 2: Durchführen einer gewöhnlichen langen Multiplikation
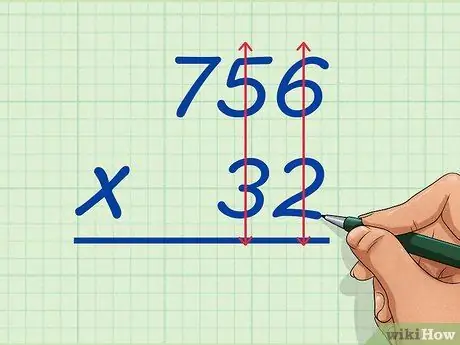
Schritt 1. Schreiben Sie die große Zahl über die kleine Zahl
Zum Beispiel würden Sie 756 und 32 multiplizieren. Schreiben Sie 756 über 32 und achten Sie darauf, dass die Einer- und Zehner-Werte der beiden Zahlen übereinstimmen, sodass die 6 von 756 über der 2 von 32 und die 5 von 756 darüber liegt die 3 von 32 usw.. Dies wird es Ihnen erleichtern, sich den langen Multiplikationsprozess vorzustellen.
Grundsätzlich beginnen Sie, 2 von 32 mit allen 756 zu multiplizieren und dann 3 von 32 mit allen 756 zu multiplizieren. Aber tun Sie das noch nicht
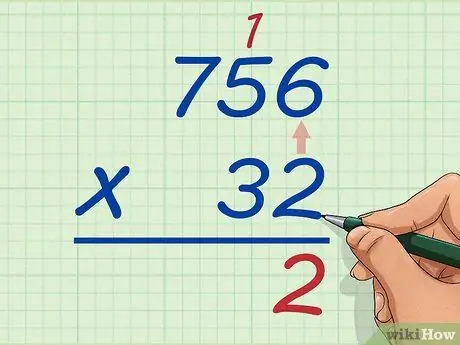
Schritt 2. Multiplizieren Sie die Einerstelle der unteren Zahl mit der Einerstelle der oberen Zahl
Nehmen Sie 2 von 32 und multiplizieren Sie es mit 6 von 756. Das Produkt von 6 und 2 ist 12. Schreiben Sie die Einerstelle 2 unter die Einerstelle und bewegen Sie 1 über die 5. Grundsätzlich schreiben Sie, was auch immer das Produkt in der Einerstelle, und wenn eine Zahl an der Zehnerstelle steht, müssen Sie sie über die Zahl links von der obersten Zahl, die Sie gerade multipliziert haben, verschieben. Sie haben 2 unter 6 und 2.

Schritt 3. Multiplizieren Sie die Einerstelle der unteren Zahl mit der Zehnerstelle der oberen Zahl
Multiplizieren Sie nun 2 und 5 mit 10. Addieren Sie die oben geschriebene 1 zu 5 zu 10, um 11 zu erhalten, und schreiben Sie dann die 1 neben die 2 im Antwortabschnitt. Sie müssen die Zahl 1 an die Zehnerstelle über 7 verschieben.

Schritt 4. Multiplizieren Sie die Einerstelle der unteren Zahl mit den Hundertern der oberen Zahl
Jetzt multiplizieren Sie 2 mit 7 zu gleich 14. Dann addieren Sie die notierte 1 zu 14, um 15 zu ergeben. Verschieben Sie den Zehnerwert nicht, da es für diese Reihe keine multiplizierten Zahlen mehr gibt. Schreiben Sie einfach 15 in den Antwortabschnitt.
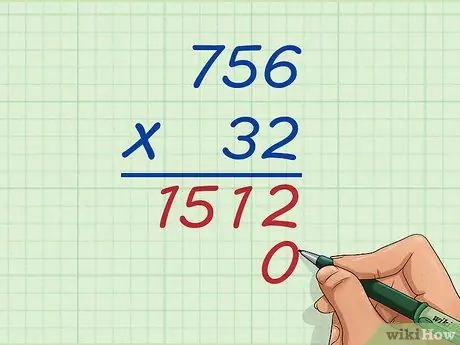
Schritt 5. Schreiben Sie 0 in die Einheitenspalte unter der ersten Multiplikationsantwort
Jetzt multiplizieren Sie die Zehnerstelle von 32, die 3 ist, mit allen 756, also schreiben Sie eine 0 unter die 2 von 1512, bevor Sie mit der Multiplikation beginnen, da Sie mit der Zehnerstelle beginnen. Wenn Sie die Hunderter mit der obersten Ziffer multiplizieren, müssen Sie zwei Nullen aufschreiben und so weiter.
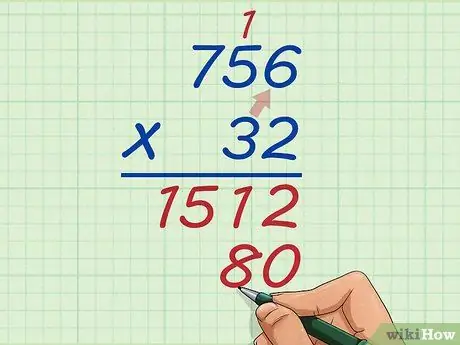
Schritt 6. Multiplizieren Sie die Zehnerstelle der unteren Zahl mit der Einerstelle der oberen Zahl
Multiplizieren Sie nun 3 mit 6 gleich 18. Platzieren Sie erneut die 8 neben der 0 und bewegen Sie die 1 über 5.

Schritt 7. Multiplizieren Sie die Zehnerzahl der unteren Zahl mit der Zehnerzahl der oberen Zahl
Multiplizieren Sie 3 mit 5. Das Ergebnis ist 15, aber Sie müssen die zuvor geschriebene 1 addieren, damit es 16 wird. Schreiben Sie die Zahl 6 in den Antwortabschnitt und verschieben Sie die Zahl 1 über 7.

Schritt 8. Multiplizieren Sie die Zehnerzahl der unteren Zahl mit den Hundertern der oberen Zahl
Multiplizieren Sie 3 mit 7 gleich 21. Addieren Sie die zuvor geschriebene Zahl 1, um 22 zu erhalten. Sie müssen die Zehnerzahl 2 nicht von 22 verschieben, da es keine Zahlen mehr gibt, die multipliziert werden können, also können Sie sie einfach als nächstes aufschreiben zur Nummer 6.
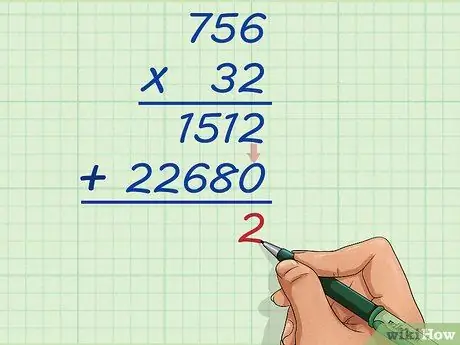
Schritt 9. Addieren Sie die Einheitswerte der beiden Multiplikationsergebnisse
Jetzt müssen Sie nur noch 1512 und 22680 addieren. Zuerst addieren Sie 2 mit 0 gleich 2. Schreiben Sie das Ergebnis in die Einheitenspalte.
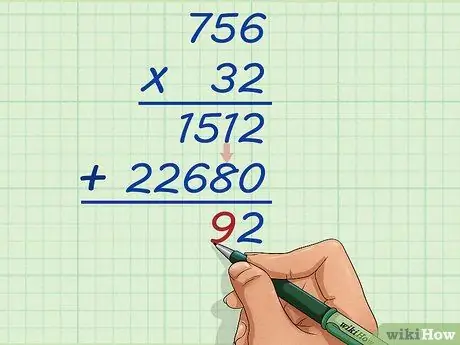
Schritt 10. Addieren Sie die zweiten Zehner des Produkts
Die Addition von 1 und 8 ergibt nun 9. Schreiben Sie 9 links von der Zahl 2.

Schritt 11. Addieren Sie die zweiten Hunderter der Multiplikationsergebnisse
Die Summe von 5 und 6 ist 11. Schreiben Sie die Zahl 1 an die Einerstelle und verschieben Sie die Zehnerzahl 1 über die 1, die ganz links vom ersten Produkt steht.

Schritt 12. Addieren Sie die Tausender der beiden Multiplikationsergebnisse
Addiere 1 mit 2 gleich 3 und addiere dann die Zahl 1, die du vorher geschrieben hast, so dass sie 4 wird. Schreibe es auf.
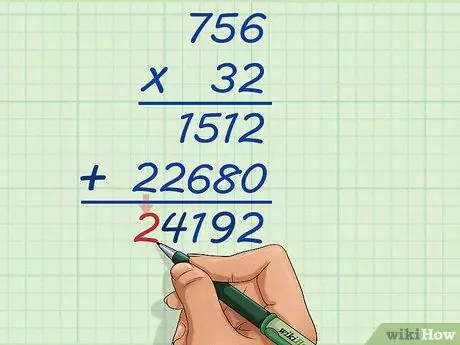
Schritt 13. Addieren Sie die Zehntausende der beiden Multiplikationsergebnisse
Die erste Zahl hat nicht den Wert von Zehntausenden und die zweite Zahl hat den Wert 2. Also addiere 0 und 2 zu 2 und schreibe sie auf. Ihre endgültige Antwort lautet 24.192.

Schritt 14. Überprüfen Sie Ihre Antworten mit einem Taschenrechner
Wenn Sie Ihre Arbeit überprüfen möchten, verwenden Sie einen Taschenrechner, um Ihre Antworten zu überprüfen. Angeblich entspricht 756 mal 32 24.192. Sie sind damit fertig!
Methode 2 von 2: Multiplikation verkürzen

Schritt 1. Schreiben Sie das Problem auf
Angenommen, Sie multiplizieren 325 mit 12. Schreiben Sie es auf. Eine Zahl muss rechts von der anderen Zahl stehen, nicht darunter.
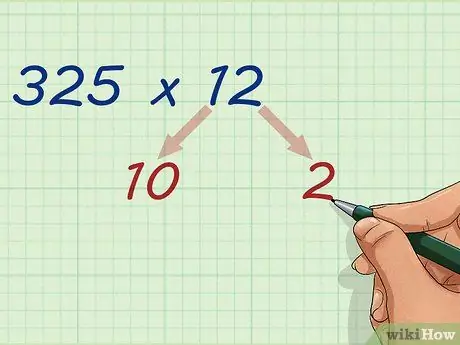
Schritt 2. Teilen Sie die kleinere Zahl in Zehner und Einer
Lassen Sie die Zahl 325 in Ruhe und teilen Sie 12 durch 10 und 2. Die 1 steht an der Zehnerstelle, also müssen Sie nach der Division immer 0 hinzufügen, und da 2 an der Einerstelle steht, können Sie einfach die Zahl 2 aufschreiben.

Schritt 3. Multiplizieren Sie die große Zahl mit der Zahl an der Zehnerstelle
Nun multiplizieren Sie 325 mit 10. Alles, was Sie tun müssen, ist am Ende eine Null hinzuzufügen, so dass das Ergebnis 3250 ist.

Schritt 4. Multiplizieren Sie die große Zahl mit der Zahl an der Einerstelle
Nun multiplizieren Sie 325 mit 2. Sie können sich das vorstellen und erhalten 650, weil 300 mal 2 gleich 600 und 25 mal 2 gleich 50 ist. Addiere 600 und 50 zu 650.
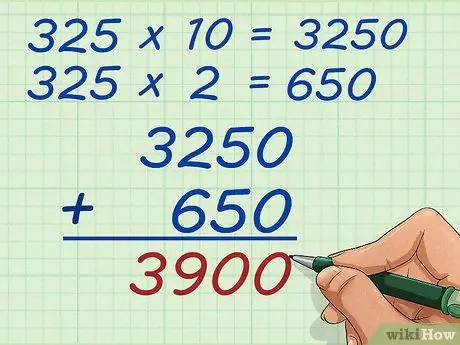
Schritt 5. Fügen Sie die beiden Produkte zusammen
Jetzt addieren Sie einfach 3250 und 650. Sie können sie mit der altmodischen Additionsmethode addieren. Schreiben Sie 3250 über 650 und führen Sie die Addition durch. Sie erhalten 3.900 Ergebnisse. Dies ist das gleiche wie bei der regulären langen Multiplikationsmethode, aber das Teilen einer Zahl in Zehner- und Einer-Werte lässt Sie sie visualisieren und vermeidet, Zahlen zu sehr zu multiplizieren und zu verschieben. Beide Wege führen zum gleichen Ergebnis und es liegt an Ihnen, welcher Weg für Sie schneller ist.
Tipps
- Üben Sie zuerst mit kurzen, einfachen Zahlen.
- Achten Sie darauf, Ihre Zahlen in die richtige Spalte einzutragen!
- Vergessen Sie nicht, Ihren Zehnerwert zu verschieben, sonst ist das Ergebnis falsch.
- Setzen Sie immer eine 0 am Ende der Zehner. In Hunderter setzen Sie ZWEI Nullen und so weiter. Überprüfen Sie auch Ihre Arbeit sorgfältig und verwenden Sie einen Taschenrechner, um die Antworten zu berechnen. Verwenden Sie jedoch keinen Taschenrechner, um Antworten zu berechnen.
- Bei Zahlen mit mehr als 2 Ziffern gehen Sie folgendermaßen vor: Multiplizieren Sie zuerst die obige Zahl mit den Einheiten, dann addieren Sie Null und multiplizieren mit Zehner, dann addieren Sie zwei Nullen und multiplizieren mit Hunderten, dann addieren Sie drei Nullen und multiplizieren mit Tausenden und so weiter. Addiere alle Zahlen.






