Eine Matrix ist eine rechteckige Anordnung von Zahlen, Symbolen oder Ausdrücken in Zeilen und Spalten. Um eine Matrix zu multiplizieren, müssen Sie die Elemente (oder Zahlen) in der ersten Zeile der Matrix mit den Elementen in der zweiten Zeile der Matrix multiplizieren und das Produkt addieren. Sie können Matrizen mit nur wenigen einfachen Schritten multiplizieren, die eine korrekte Addition, Multiplikation und Platzierung der Ergebnisse erfordern.
Schritt
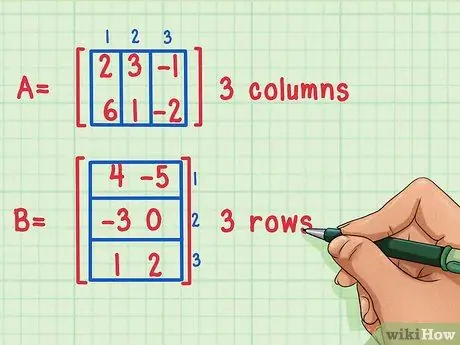
Schritt 1. Stellen Sie sicher, dass die Matrizen multiplizierbar sind
Sie können eine Matrix nur multiplizieren, wenn die Anzahl der Spalten der ersten Matrix gleich der Anzahl der Zeilen der zweiten Matrix ist.
Diese Matrizen können multipliziert werden, da die erste Matrix, Matrix A, 3 Spalten hat, während die zweite Matrix, Matrix B, 3 Zeilen hat
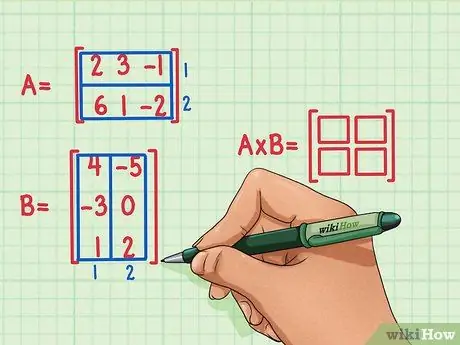
Schritt 2. Markieren Sie die Abmessungen des Matrixprodukts
Erstellen Sie eine neue, leere Matrix, die die Dimensionen des Produkts der beiden Matrizen markiert. Die Matrix, die das Produkt von Matrix A und Matrix B darstellt, hat dieselbe Anzahl von Zeilen wie die erste Matrix und dieselbe Anzahl von Spalten wie die zweite Matrix. Sie können leere Kästchen zeichnen, um die Anzahl der Zeilen und Spalten in dieser Matrix anzuzeigen.
- Matrix A hat 2 Zeilen, also hat das Ergebnis der Multiplikation der Matrix 2 Zeilen.
- Matrix B hat 2 Spalten, so dass das Ergebnis der Multiplikation der Matrix 2 Spalten hat.
- Das Ergebnis des Matrixprodukts hat 2 Zeilen und 2 Spalten.
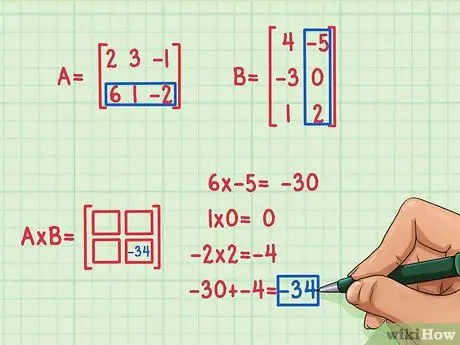
Schritt 3. Finden Sie das Ergebnis des ersten Punktprodukts
Um das Ergebnis des ersten Punktprodukts zu ermitteln, müssen Sie das erste Element in der ersten Zeile mit dem ersten Element in der ersten Spalte, das zweite Element in der ersten Zeile mit dem zweiten Element in der ersten Spalte und das dritte Element in multiplizieren die erste Zeile durch das dritte Element in der ersten Spalte. Addiere dann die Multiplikationsergebnisse, um zu finden Punktprodukt (Punkt).
Angenommen, Sie haben sich entschieden, zuerst die Elemente in der zweiten Zeile und zweiten Spalte (unten rechts) des Matrixprodukts zu berechnen. So machen Sie es:
- 6 x -5 = -30
- 1 x 0 = 0
- -2 x 2 = -4
- -30 + 0 + (-4) = -34
-
Das Ergebnis des Skalarprodukts ist -34 und dieses Ergebnis wird unten rechts in das Matrixprodukt geschrieben.
Wenn Sie eine Matrix multiplizieren, wird das Skalarprodukt in die Zeilenposition der ersten Matrix und die Spaltenposition der zweiten Matrix geschrieben. Wenn Sie beispielsweise das Skalarprodukt der unteren Zeile von Matrix A und der rechten Spalte von Matrix B kennen, wird die Antwort -34 in die untere Zeile und rechte Spalte des Matrixprodukts geschrieben
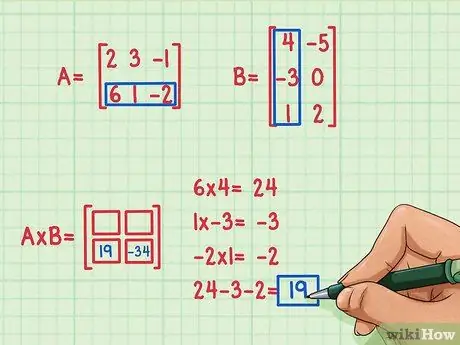
Schritt 4. Finden Sie das Ergebnis des zweiten Punktprodukts
Angenommen, Sie möchten den Term unten links im Matrixprodukt finden. Um diesen Begriff zu finden, müssen Sie nur die Elemente in der unteren Zeile der ersten Matrix mit den Elementen in der ersten Spalte der zweiten Matrix multiplizieren und dann addieren. Verwenden Sie die gleiche Methode wie beim Multiplizieren der ersten Zeile und Spalte – finden Sie erneut Punktprodukt (Do t)seine.
- 6 x 4 = 24
- 1 x (-3) = -3
- (-2) x 1 = -2
- 24 + (-3) + (-2) = 19
- Das Ergebnis des Skalarprodukts ist -19 und dieses Ergebnis wird unten links in das Matrixprodukt geschrieben.
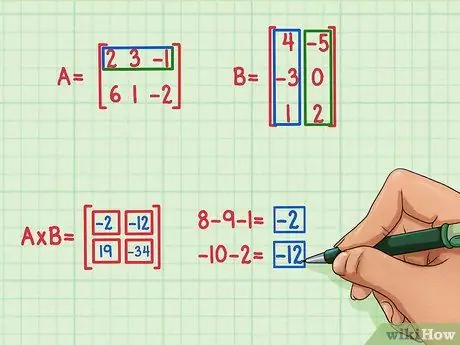
Schritt 5. Suchen Sie die anderen zwei Punktprodukte
Um den Term oben links im Matrixprodukt zu finden, suchen Sie zunächst das Punktprodukt der oberen Reihe von Matrix A und der linken Spalte von Matrix B. So gehen Sie vor:
- 2 x 4 = 8
- 3 x (-3) = -9
- (-1) x 1 = -1
- 8 + (-9) + (-1) = -2
-
Das Ergebnis des Skalarprodukts ist -2 und dieses Ergebnis wird oben links in das Matrixprodukt geschrieben.
Um den Term oben rechts im Matrixprodukt zu finden, suchen Sie einfach nach dem Punktprodukt der oberen Reihe von Matrix A und der rechten Spalte von Matrix B. So gehen Sie vor:
- 2 x (-5) = -10
- 3 x 0 = 0
- (-1) x 2 = -2
- -10 + 0 + (-2) = -12
- Das Skalarprodukt ist -12 und dieses Ergebnis wird oben rechts in das Matrixprodukt geschrieben.
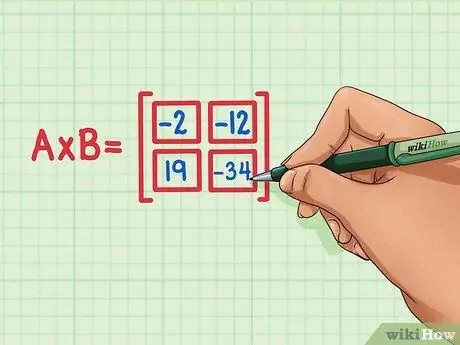
Schritt 6. Stellen Sie sicher, dass sich die Vierpunktprodukte an der richtigen Stelle im Matrixprodukt befinden
19 muss unten links sein, -34 muss unten rechts sein, -2 muss oben links sein und -12 muss oben rechts sein.
Tipps
- Die Verwendung von Liniensegmenten und keine Verwendung von Linien kann die falsche Antwort geben. Wenn eine Zeile, die eine Zeile darstellt, eine Verlängerung erfordert, um eine Spalte zu überqueren, dann verlängern Sie sie! Dies ist nur eine Visualisierungstechnik, mit der Sie leichter erkennen können, welche Zeilen und Spalten Sie verwenden müssen, um mit jedem Element des Produkts zu arbeiten.
- Das Produkt der beiden Matrizen ergibt die Anzahl der Zeilen gleich der Anzahl der Zeilen der ersten Matrix und die Anzahl der Spalten gleich der Anzahl der Spalten der zweiten Matrix.
- Schreiben Sie Ihre Summe auf. Das Multiplizieren von Matrizen erfordert viele Berechnungen und es ist sehr leicht, abgelenkt zu werden und zu vergessen, welche Zahl Sie multiplizieren.
