IQR ist der Interquartilsabstand oder der Quartilswurzelbereich eines Datensatzes. IQR wird in der statistischen Analyse verwendet, um Rückschlüsse auf einen Datensatz zu ziehen. IQR wird häufiger als Bereich verwendet, da IQR nicht die äußersten Daten enthält. Lesen Sie weiter, um zu erfahren, wie Sie den IQR finden!
Schritt
Methode 1 von 3: IQR verstehen
Schritt 1. Verstehen Sie, wie man IQR verwendet
Im Grunde ist IQR eine Möglichkeit, die Verbreitung einer Reihe von Zahlen zu verstehen. Der Wurzelquartilbereich ist definiert als die Differenz zwischen dem oberen Quartil (25 % oben) und dem unteren Quartil (25 % unten) des Datensatzes.
Spitze:
Das untere Quartil wird normalerweise als Q1 und das obere Quartil als Q3 geschrieben – was technisch gesehen den Mittelpunkt der Daten zu Q2 und den höchsten Punkt zu Q4 macht.
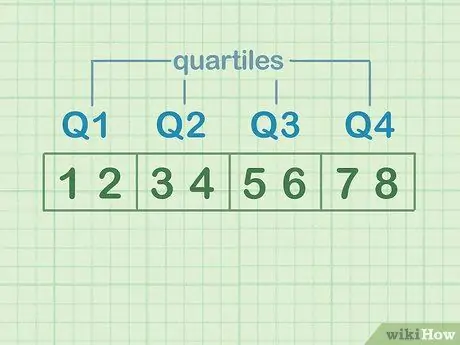
Schritt 2. Verstehen Sie die Quartile
Um Quartile zu veranschaulichen, teilen Sie die Zahlenmenge in vier gleiche Teile. Jeder dieser Teile ist ein „Quartil“. Angenommen, die Datensätze sind: 1, 2, 3, 4, 5, 6, 7, 8.
- 1 und 2 sind das erste Quartil oder Q1
- 3 und 4 sind das zweite Quartil oder Q2
- 5 und 6 sind das dritte Quartil oder Q3
- 7 und 8 sind das vierte Quartil oder Q4
Schritt 3. Lernen Sie die Formel
Um die Differenz zwischen dem oberen und dem unteren Quartil zu ermitteln, müssen Sie das 75. Perzentil vom 25. Perzentil subtrahieren.
Die Formel lautet: Q3 – Q1 = IQR
Methode 2 von 3: Zusammenstellen des Datensatzes
Schritt 1. Sammeln Sie Ihre Daten
Wenn Sie IQR im Unterricht und in Tests studieren, erhalten Sie möglicherweise einen bereits vorbereiteten Datensatz, zum Beispiel 1, 4, 5, 7, 10. Dies ist Ihr Datensatz – die Zahlen, mit denen Sie arbeiten werden. Sie können jedoch Ihre eigenen Zahlen aus Tabellenfragen oder Story-Problemen erstellen.
Stellen Sie sicher, dass jede Zahl dasselbe darstellt:
B. die Anzahl der Eier in jedem Nest einer definierten Vogelpopulation oder die Anzahl der Parkplätze, die sich in jedem Haus in einem bestimmten Block befinden.
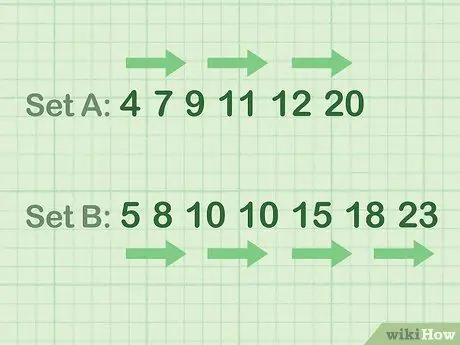
Schritt 2. Sortieren Sie Ihre Daten in aufsteigender Reihenfolge
Mit anderen Worten: Ordne die Zahlen von der kleinsten zur größten. Verwenden Sie die Hinweise aus den folgenden Beispielen.
- Beispiel für gerade Zahlendaten (Set A): 4 7 9 11 12 20
- Beispiel für ungeradzahlige Daten (Set B): 5 8 10 10 15 18 23
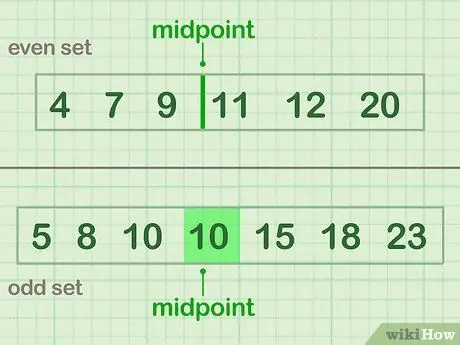
Schritt 3. Teilen Sie die Daten in zwei Teile auf
Um die Hälfte zu teilen, suchen Sie den Mittelpunkt Ihrer Daten: die Zahl oder Zahlen, die sich in der Mitte des Datensatzes befinden. Wenn Sie eine ungerade Anzahl von Daten haben, wählen Sie die Zahl, die sich genau in der Mitte befindet. Bei einer geraden Anzahl von Daten liegt der Mittelpunkt zwischen den beiden mittleren Zahlen.
- Ein gerades Beispiel (Set A), das einen Mittelpunkt zwischen 9 und 11 hat: 4 7 9 | 11 12 20
- Ein ungerades Beispiel (Set B), das einen Mittelpunkt des Wertes (10) hat: 5 8 10 (10) 15 18 23
Methode 3 von 3: Berechnung des IQR
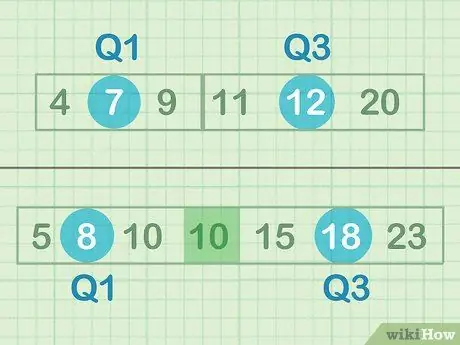
Schritt 1. Ermitteln Sie den Median Ihrer unteren und oberen Hälfte der Daten
Der Median ist der "Mittelpunkt" oder die Zahl, die sich in der Mitte einer Reihe von Zahlen befindet. In diesem Fall suchen Sie nicht nach dem Mittelpunkt aller Zahlen, sondern nach dem relativen Mittelpunkt der oberen und unteren Datenteilmengen. Wenn Sie eine ungerade Anzahl von Daten haben, schließen Sie die mittlere Zahl nicht ein – in Satz B müssen Sie beispielsweise keine einzelne 10 angeben.
-
Gerades Beispiel (Set A):
- Median der unteren Hälfte der Daten = 7 (Q1)
- Median der oberen Hälfte der Daten = 12 (Q3)
-
Seltsames Beispiel (Set B):
- Median der unteren Hälfte der Daten = 8 (Q1)
- Median der oberen Hälfte der Daten = 18 (Q3)
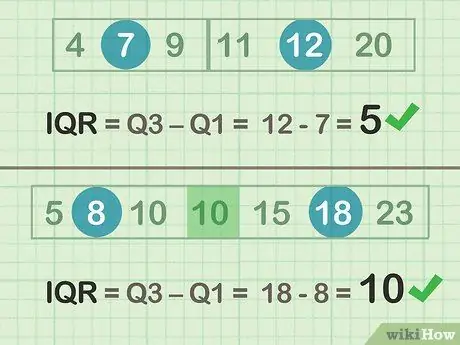
Schritt 2. Subtrahieren Sie Q3-Q1, um den IQR zu bestimmen
Jetzt wissen Sie, wie viele Zahlen zwischen dem 25. und 75. Perzentil liegen. Sie können diese Zahl verwenden, um die Streuung von Daten zu verstehen. Wenn ein Test beispielsweise eine Höchstpunktzahl von 100 hat und der IQR der Punktzahl 5 beträgt, können Sie davon ausgehen, dass die meisten Testpersonen fast das gleiche Verständnis haben, da die Spanne der Höhen und Tiefen nicht sehr groß ist. Wenn der IQR eines Testergebnisses jedoch 30 beträgt, werden Sie sich vielleicht fragen, warum manche Menschen so hoch und andere so niedrig abschneiden.
- Gerades Beispiel (Set A): 12 -7 = 5
- Ungerades Beispiel (Set B): 18 – 8 = 10
Tipps
Es ist wichtig, dies selbst zu lernen. Es gibt jedoch mehrere Online-IQR-Rechner, mit denen Sie Ihre Arbeit überprüfen können. Verlassen Sie sich nicht zu sehr auf Taschenrechner-Apps, wenn Sie dies im Unterricht lernen! Wenn Sie aufgefordert werden, den IQR in einem Test nachzuschlagen, müssen Sie wissen, wie Sie ihn manuell finden können
Verwandte WikiHow
- So erkennen Sie Ausreißer
- So berechnen Sie die Reichweite eines Datensatzes
- Wie erstelle ich ein Box- und Zeltdiagramm?
