Solange Sie das Maß der anderen beiden Winkel kennen, ist es einfach, den dritten Winkel eines Dreiecks zu finden. Sie müssen nur die Summe der beiden Winkel um 180 Grad subtrahieren. Es gibt jedoch auch andere Möglichkeiten, den dritten Winkel eines Dreiecks zu finden, wenn die Form des Problems etwas anders als üblich ist. Wenn Sie wissen möchten, wie Sie den dritten Winkel eines Dreiecks finden, folgen Sie der folgenden Anleitung.
Schritt
Methode 1 von 3: Verwenden der Maße der anderen beiden Winkel
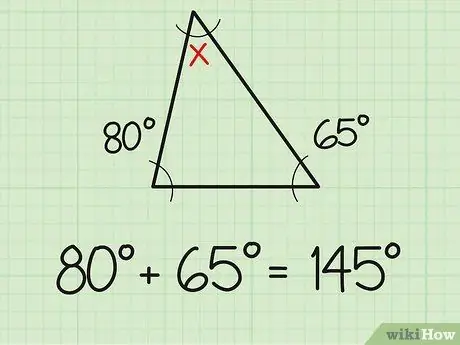
Schritt 1. Addieren Sie die beiden bekannten Winkel
Eine Tatsache, die Sie wissen sollten, ist, dass die Summe der drei Winkel eines Dreiecks immer 180 Grad beträgt. Wenn Sie also bereits das Maß der beiden Winkel eines Dreiecks kennen, ist das Finden des dritten Winkels so einfach wie einfache Additions- und Subtraktionsaufgaben. Addieren Sie zunächst die beiden bereits bekannten Winkelmaße. Zwei bekannte Winkel messen beispielsweise 80 und 65 Grad. Addieren Sie die beiden zusammen (80 + 65), und Sie erhalten 145 Grad.
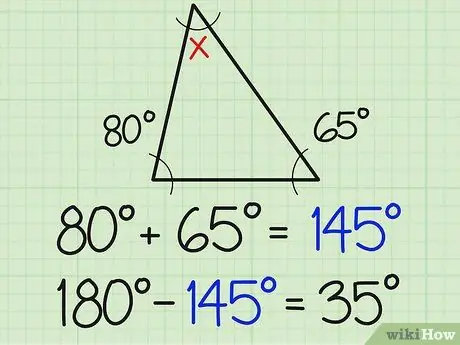
Schritt 2. Teilen Sie diese Zahl durch 180
Die Summe der drei Winkel eines Dreiecks beträgt immer 180 Grad. Daher muss der dritte Winkel 180 betragen, wenn er zur Summe der beiden bekannten Winkelmaße addiert wird. Im obigen Beispiel bedeutet dies 180-154=35.
Schritt 3. Schreiben Sie Ihre Antwort
Jetzt haben Sie die Antwort auf den dritten Winkel (im Beispiel 35 Grad). Wenn Sie immer noch Zweifel haben, sehen Sie selbst. Addieren Sie die drei Winkel zusammen, und Sie sollten ein Ergebnis von 180 erhalten. Wenn Sie dies nicht tun, ist Ihre Berechnung falsch. Für dieses Beispiel 80+65+35=180. Wenn es richtig ist, bedeutet dies, dass Sie das Problem gelöst haben.
Methode 2 von 3: Verwenden von Variablen
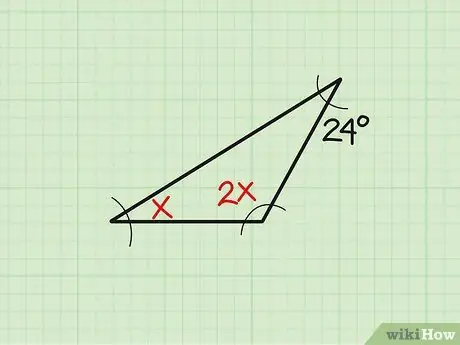
Schritt 1. Schreiben Sie das Problem auf
Manchmal wird die Größe des vorhandenen Winkels in variabler Form angezeigt. Nehmen wir dieses Beispiel: „Finde den Winkel „x“eines Dreiecks, wenn die drei Winkel „x“, „2x“bzw. 24 messen.“Schreiben Sie zuerst das Problem auf.
Schritt 2. Addieren Sie alle Winkelmaße
Das Prinzip, an das Sie sich erinnern müssen, bleibt das gleiche. Addieren Sie also zunächst die drei Winkel in der Aufgabe, nämlich "x+2x+24 = 3x+24".
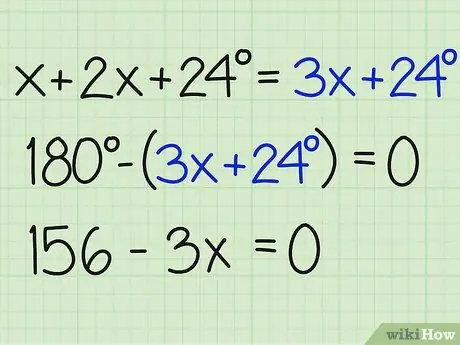
Schritt 3. Teilen Sie die Summe der Winkel durch 180
Unterscheiden Sie diese Zahl nun um 180 Grad, um x zu finden und die Antwort auf das Problem zu finden. Stellen Sie sicher, dass Sie die Gleichung gleich Null beenden. So ist es geschrieben:
- 180-(3x+24) = 0
- 180-3x-24 = 0
- 156-3x = 0
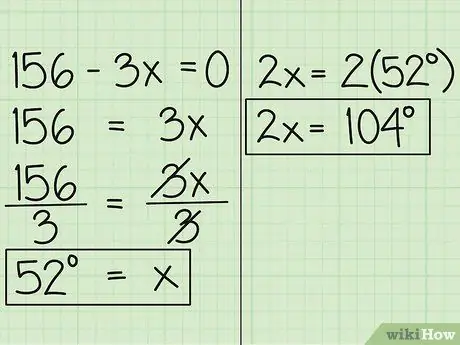
Schritt 4. Finden Sie den Wert von x
Verschieben Sie nun die Variable auf die andere Seite der Gleichung und Sie erhalten 156 = 3x. Dann dividiere die Gleichung durch 3, so dass du x = 52 erhältst. Dies bedeutet, dass das Maß des in x ausgedrückten Winkels 52 Grad beträgt. Der andere Winkel, ausgedrückt in 2x, beträgt 52 Grad mal 2, also 104 Grad.
Schritt 5. Überprüfen Sie Ihre Ergebnisse
Wenn Sie sicherstellen möchten, dass Ihre Antwort richtig ist, addieren Sie einfach die drei Winkelmaße, auf die Sie bereits die Antwort gefunden haben. Wenn das Ergebnis 180 ist, bedeutet dies, dass Ihre Antwort richtig ist. Für dieses Beispiel 52+104+24 = 180.
Methode 3 von 3: Andere Methoden verwenden
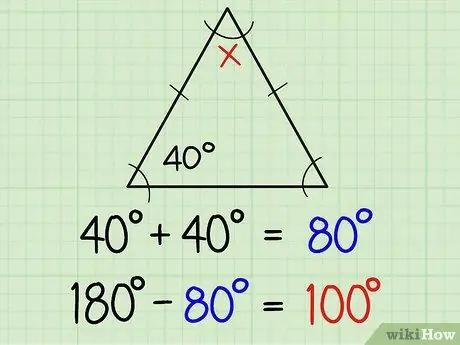
Schritt 1. Bestimmen Sie die Winkel eines gleichschenkligen Dreiecks
Ein gleichschenkliges Dreieck hat zwei gleiche Seiten und zwei gleiche Winkel. Zwei gleiche Seiten werden normalerweise mit einem kleinen Strich in der Mitte der Seitenlinie markiert, was bedeutet, dass die beiden gegenüberliegenden Winkel auf der Linie das gleiche Maß haben. Wenn Sie die Größe eines Winkels bereits kennen, kennen Sie automatisch den anderen Winkel. Hier ist eine weitere Erklärung:
Wenn einer der gleichen Winkel 40 Grad beträgt, beträgt der andere 40 Grad. Auf diese Weise finden Sie alle drei Winkel mit der Differenz zwischen der Summe von 40+40 (also 80) und 180, also 180-80 = 100
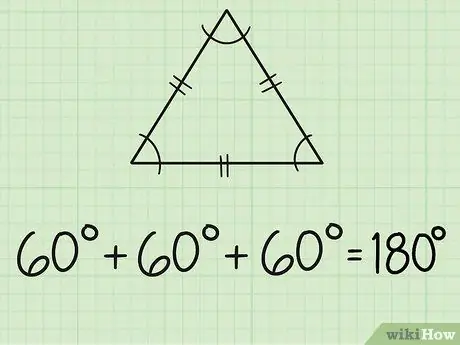
Schritt 2. Finden Sie die Winkel eines gleichseitigen Dreiecks
Ein gleichseitiges Dreieck hat drei gleiche Seiten und drei gleiche Winkel. Jede Seite ist normalerweise mit zwei kurzen Strichen in der Mitte gekennzeichnet. Da alle drei Winkel gleich sind, messen alle Winkel 60 Grad, denn 180/3 = 60.
Schritt 3. Finden Sie den dritten Winkel in einem rechtwinkligen Dreieck
Angenommen, Sie erhalten ein rechtwinkliges Dreieck mit einem der spitzen Winkel von 30 Grad. Da das Dreieck ein rechter Winkel ist, bedeutet dies, dass einer der Winkel, nämlich der rechte Winkel, 90 Grad messen muss. Dann wende das Dreiecksprinzip an, die Differenz der Summe der beiden Winkel (90+30 = 120) mal 180, dann erhältst du 180-120 = 60 Grad.
