- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:03.
- Zuletzt bearbeitet 2025-06-01 06:05.
Das dezimale Zahlensystem (zur Basis zehn) hat zehn mögliche Werte (0, 1, 2, 3, 4, 5, 6, 7, 8 oder 9) für jede Zahlenposition. Im Gegensatz dazu hat das binäre Zahlensystem (zur Basis zwei) für jede Zahlenposition nur zwei mögliche Werte, die durch 0 und 1 dargestellt werden. Da das binäre Zahlensystem die interne Sprache elektronischer Computer ist, wissen ernsthafte Computerprogrammierer, wie man vom dezimalen in das binäre Zahlensystem umwandelt. Befolgen Sie diese einfachen Schritte und erfahren Sie, wie Sie diese Konvertierung meistern.
Schritt
Methode 1 von 2: Kurze Division durch zwei mit Rest

Schritt 1. Bestimmen Sie das Problem
Konvertieren wir für dieses Beispiel die Dezimalzahl 15610 eine binäre Zahl sein. Schreiben Sie die Dezimalzahl als zu teilende Zahl in das invertierte Divisionssymbol. Schreiben Sie die Basis des Ziel-Zahlensystems (in diesem Beispiel „2“für binär) als den außerhalb der Kurve liegenden Teiler des Divisionssymbols.
- Diese Methode ist beim Zeichnen auf Papier viel einfacher zu verstehen und für Anfänger viel einfacher, da sie nur durch zwei geteilt wird.
- Um Verwechslungen vor und nach der Umrechnung zu vermeiden, notieren Sie sich für jede Zahl die Basiszahl des zu berechnenden Zahlensystems tiefgestellt (Kleinbuchstaben unter normalen Buchstaben als Unterscheidungszeichen). In diesem Beispiel hat die Dezimalzahl den Index 10 und die Binärzahl den Index 2.

Schritt 2. Führen Sie die Aufteilung durch
Schreiben Sie die ganzzahlige Antwort (Quotient) unter das lange Divisionssymbol und schreiben Sie den Rest (0 oder 1) rechts von der geteilten Zahl.
Da wir durch zwei dividieren, ist bei einer geraden Zahl der Rest 0 und bei einer ungeraden Zahl ist der Rest 1

Schritt 3. Fahren Sie mit dem Dividieren fort, bis es Null erreicht
Fahren Sie bergab, teilen Sie jeden neuen Quotienten durch zwei und schreiben Sie den Rest rechts von jeder geteilten Zahl. Stoppen Sie, wenn der Quotient Null ist.

Schritt 4. Schreiben Sie die neue Binärzahl auf
Lesen Sie ausgehend von der niedrigsten Restzahl die Reihenfolge der Reste in aufsteigender Reihenfolge nach oben. In diesem Beispiel sollten Sie das Ergebnis 10011100 erhalten. Dies ist das binäre Äquivalent der Dezimalzahl 156. Oder, wenn es mit seinem numerischen Basisindex geschrieben wird: 15610 = 100111002.
Diese Methode kann geändert werden, um von der Dezimalbasis in eine beliebige Zahlenbasis umzuwandeln. Der Divisor ist 2, da die Basis des Zielnummernsystems die Basis 2 (binär) ist. Wenn die Basis des Zielrufnummernsystems eine andere Basis ist, ersetzen Sie die Basis-2-Nummer bei dieser Methode durch die entsprechende Basisnummer. Wenn die Zielbasis beispielsweise die Basis 9 ist, ersetzen Sie die Nummer der Basis 2 durch 9. Das Endergebnis wird direkt in Form der Zielbasisnummer angezeigt
Methode 2 von 2: Ableiten von Zweierpotenzen und Subtraktion

Schritt 1. Beginnen Sie mit dem Erstellen einer Tabelle
Notieren Sie die Potenzen der beiden Basiszahlen in der "Tabelle 2 Basis" von rechts nach links. Beginnen Sie bei 20, schreiben Sie es als „1“. Erhöhen Sie den Rang um 1 für jeden Rang. Vervollständigen Sie die Tabelle, bis Sie eine Zahl erhalten, die der Zahl des Dezimalzahlensystems, das Sie berechnen, am nächsten kommt. Konvertieren wir für dieses Beispiel die Dezimalzahl 15610 eine binäre Zahl sein.

Schritt 2. Finden Sie die Zahl mit der größten Potenz der Basiszahl 2
Wählen Sie aus der Tabelle die größte Zahl aus, die kleiner oder gleich der zu konvertierenden Zahl ist. Die Zahl 128 ist die Zahl mit der größten Potenz der Basiszahl 2 und ist auch kleiner als 156, also schreibe unter dieses Kästchen in der Tabelle eine Zahl "1", wobei die größte Zahl aus der Tabelle links steht (siehe Tabelle im Bild oben). Ziehen Sie dann 128 von der Anfangszahl ab, Sie erhalten: 156 - 128 = 28.
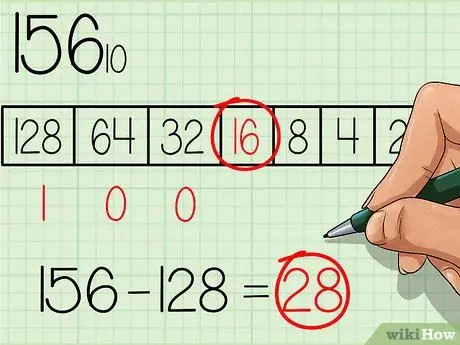
Schritt 3. Fahren Sie mit der nächst kleineren Potenz in der Tabelle fort
Gehen Sie mit der neuen Zahl (28) von links nach rechts durch die Tabelle und prüfen Sie, ob die Zahlen gleich oder kleiner als die neue Zahl sind. Die Zahl 64 ist nicht kleiner als 28, also schreiben Sie die Zahl „0“unter das Zahlenfeld 64. Fahren Sie fort, bis Sie eine Zahl finden, die kleiner oder gleich 28 ist.
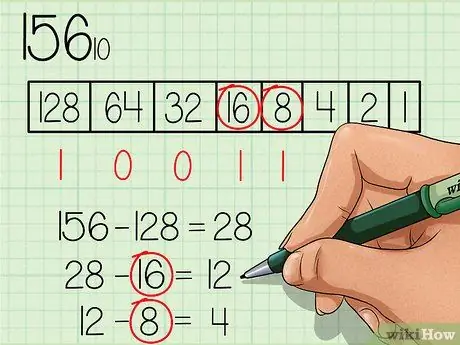
Schritt 4. Subtrahieren Sie fortlaufend jede Zahl, die kleiner oder gleich der neuen Zahl ist, und markieren Sie die Zahl „1“unter dem Kästchen für die entsprechende Zahl
Die Zahl 16 ist kleiner als 28, also schreibe die Zahl "1" unter das Zahlenfeld 16 und subtrahiere 16 von 28, so erhältst du eine neue Zahl 12. Die Zahl 8 ist kleiner als 12, also schreibe die Zahl "1" unter das Zahlenfeld 8 und subtrahiere 8 von 12, um die neue Zahl 4 zu erhalten.

Schritt 5. Fahren Sie fort, bis Sie das Ende der Tabelle erreichen
Denken Sie daran, unter jedem Kästchen eine „1“für Zahlen zu markieren, die gleich oder kleiner als die neue Zahl sind, und eine „0“unter jedem Kästchen für Zahlen, die noch größer als die neue Zahl sind.
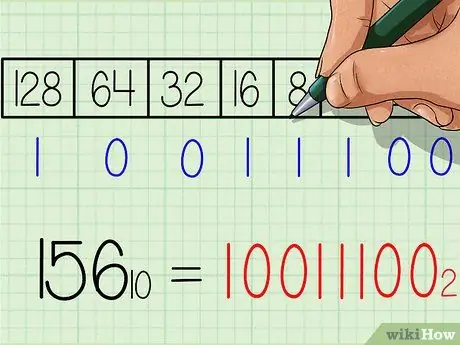
Schritt 6. Schreiben Sie die Antwort für die Binärzahl auf
Die Zahl entspricht von links nach rechts genau der Zahlenreihe „1“und „0“am unteren Rand der Tabelle. Sie sollten das Ergebnis 10011100 erhalten. Dies ist das binäre Äquivalent der Dezimalzahl 156. Oder wenn es mit einem Index geschrieben wird: 15610 = 100111002.
Das Wiederholen dieser Methode kann Ihnen helfen, sich an die Potenzen der Basis zwei zu erinnern, sodass Sie Schritt 1 überspringen können
Tipps
- Das in das Betriebssystem integrierte Rechnerprogramm kann diese Konvertierung für Sie durchführen, aber als Programmierer ist es am besten, mit einem guten Verständnis der Funktionsweise von Konvertierungen zu beginnen. Die Konvertierungsoptionen im Rechnerprogramm können sichtbar gemacht werden, indem das Menü „Ansicht“geöffnet und „Programmierer“ausgewählt wird (für Windows 7 und 8).
- Das Umrechnen in die entgegengesetzte Richtung, also vom binären in das dezimale Zahlensystem, ist in der Regel zunächst einfacher zu erlernen.
- Üben Sie oft, Dezimalzahlen in Binärzahlen umzuwandeln, um Experten zu werden.






