- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:12.
- Zuletzt bearbeitet 2025-01-23 12:15.
Das geometrische Mittel ist eine weitere Möglichkeit, den Durchschnittswert einer Reihe von Zahlen zu ermitteln, indem die Werte vor dem Ziehen der Wurzeln multipliziert werden, anstatt die Werte zu addieren und wie bei einem arithmetischen Mittel zu teilen. Das geometrische Mittel kann verwendet werden, um die durchschnittliche Rendite in der Finanzanalyse zu berechnen oder die Wachstumsrate von etwas über einen bestimmten Zeitraum anzuzeigen. Um das geometrische Mittel zu ermitteln, multiplizieren Sie alle Werte vor dem Rooten mit, was die Gesamtzahl der Zahlen in der Menge ist. Sie können auch die Logarithmus-Funktion Ihres Taschenrechners verwenden, um das geometrische Mittel zu ermitteln, wenn Sie dies bevorzugen.
Schritt
Methode 1 von 2: Ermitteln des geometrischen Durchschnitts eines Wertesatzes
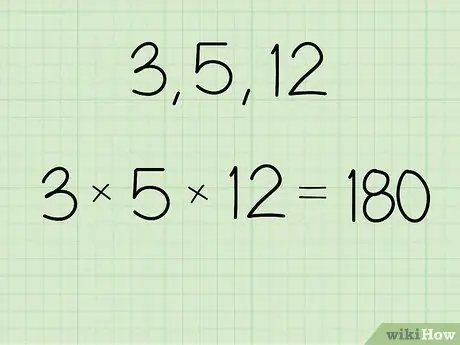
Schritt 1. Multiplizieren Sie den Wert, für den Sie den geometrischen Mittelwert ermitteln möchten
Sie können einen Taschenrechner verwenden oder manuell berechnen, um das Ergebnis zu erhalten. Schreiben Sie die Ergebnisse auf, damit Sie sie nicht vergessen.
- Wenn der Zahlensatz beispielsweise 3, 5 und 12 ist, berechnen Sie: (3 x 5 x 12) = 180.
- Wenn Sie als weiteres Beispiel das geometrische Mittel der Zahlenmenge 2 und 18 ermitteln möchten, schreiben Sie: (2 x 18) = 36.
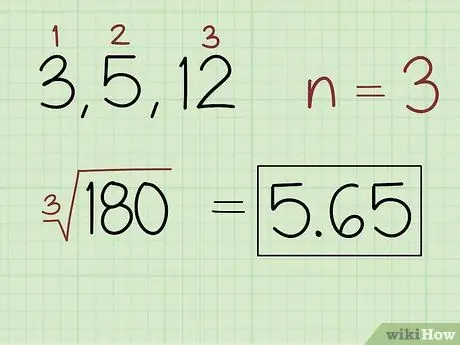
Schritt 2. Finden Sie die n-te Wurzel des Produkts, wobei n die Anzahl der Werte in der Menge ist
Zählen Sie die Anzahl der Zahlen in der Menge, um den Wert zu erhalten. Verwenden Sie die Werte, um die Wurzel anzugeben, die im Produkt verwendet werden muss. Verwenden Sie beispielsweise die Quadratwurzel, wenn die Menge 2 Zahlen enthält, die Kubikwurzel, wenn die Menge 3 Zahlen enthält, und so weiter. Benutze einen Taschenrechner, um die Gleichung zu lösen und schreibe die Antwort auf.
- Schreiben Sie beispielsweise für eine Reihe von Zahlen 3, 5 und 12: (180) 5, 65.
- Schreiben Sie im zweiten Beispiel mit der Menge aus 2 und 18: (36) = 6.
Variation:
Sie können die Wurzel auch als Exponent von 1/ schreiben, wenn es einfacher ist, auf einem Taschenrechner zu schreiben. Schreiben Sie beispielsweise für die Menge der Zahlen 3, 5 und 12 (180)1/3 statt (180).
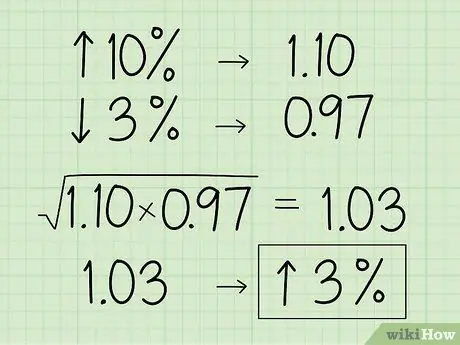
Schritt 3. Konvertieren Sie den Prozentsatz in sein Dezimalmultiplikatoräquivalent
Wenn der Zahlensatz als prozentuale Zunahme oder Abnahme geschrieben wird, versuchen Sie, den Prozentwert nicht im geometrischen Mittel zu verwenden, da die Ergebnisse nicht genau sind. Wenn sich der Prozentsatz erhöht, verschieben Sie den Dezimalpunkt um zwei Stellen nach links und addieren Sie 1. Wenn der Prozentsatz sinkt, verschieben Sie den Dezimalpunkt um 2 Stellen nach links und subtrahieren von 1.
- Angenommen, Sie möchten den geometrischen Mittelwert von Objektwerten ermitteln, der um 10 % zunimmt und dann um 3 % abnimmt.
- Wandeln Sie 10 % in eine Dezimalzahl um und addieren Sie 1 zu 1, 10.
- Wandle dann 3% in eine Dezimalzahl um und ziehe 1 ab, um 0,97 zu erhalten.
- Verwenden Sie beide Dezimalstellen, um das geometrische Mittel zu ermitteln: (1, 10 x 0,97) 1,03.
- Wandeln Sie die Zahl wieder in einen Prozentsatz um, indem Sie den Dezimalpunkt um 2 Stellen nach rechts verschieben und 1 subtrahieren, um einen Wertzuwachs von 3% zu erhalten.
Methode 2 von 2: Berechnung des geometrischen Durchschnitts mit Logarithmen

Schritt 1. Addieren Sie die logarithmischen Werte für jede Zahl im Satz
Die LOG-Funktion des Taschenrechners nimmt die Basis 10 einer Zahl und bestimmt, wie viel Sie mit 10 multiplizieren müssen, damit es der Zahl entspricht. Suchen Sie auf dem Taschenrechner nach der LOG-Funktion, die sich normalerweise auf der linken Seite der Schaltfläche befindet. Klicken Sie auf die Schaltfläche LOG und geben Sie die erste Zahl im Satz ein. Geben Sie „+“ein, bevor Sie LOG für die zweite Zahl eingeben. Trennen Sie weiterhin die LOG-Funktion für jede Zahl mit einem Pluszeichen, bevor Sie die Summe erhalten.
- Geben Sie beispielsweise für die Sätze 7, 9 und 12 log(7) + log(9) + log(12) ein und drücken Sie dann „=“auf dem Taschenrechner. Wenn die Funktion berechnet wurde, beträgt die Zahl etwa 2.878521796.
- Sie können auch jeden Logarithmus separat berechnen, bevor Sie alle zusammenzählen.
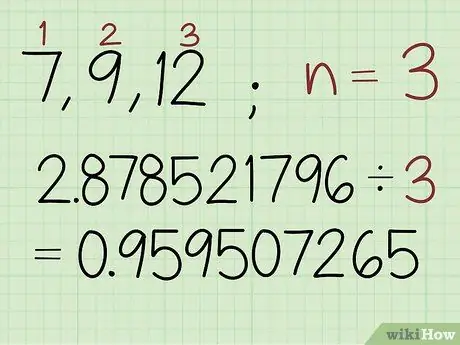
Schritt 2. Teilen Sie die Summe der logarithmischen Werte durch die Anzahl der Zahlen im Satz
Zählen Sie die Anzahl der Werte im Satz und teilen Sie die zuvor erhaltene Zahl durch diese Zahl. Das Ergebnis ist der Logarithmus des geometrischen Mittels.
In diesem Beispiel gibt es 3 Zahlen im Set, also geben Sie ein: 2, 878521796 / 3 0, 959507265

Schritt 3. Ermitteln Sie den Antilog des Quotienten, um den geometrischen Mittelwert zu bestimmen
Die Antilog-Funktion ist die Umkehrung der LOG-Funktion auf dem Taschenrechner und wandelt den Wert zurück zur Basis 10. Suchen Sie nach dem Symbol „10“x“auf dem Taschenrechner, was normalerweise eine sekundäre Funktion der LOG-Taste ist. Drücken Sie die Taste „ 2nd “in der oberen linken Ecke des Taschenrechners, gefolgt von der LOG-Taste, um Antilog zu aktivieren. Geben Sie den im letzten Schritt gefundenen Quotienten ein, bevor Sie die Gleichung lösen.
In diesem Beispiel zeigt der Rechner an: 10(0, 959507265) ≈ 9, 11.
Tipps
- Sie können das geometrische Mittel negativer Zahlen nicht finden.
- Alle Mengen mit 0 haben ein geometrisches Mittel von 0.






