- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:12.
- Zuletzt bearbeitet 2025-01-23 12:14.
Im Maschinenbau ist das Übersetzungsverhältnis ein direktes Maß für die Drehzahl von zwei oder mehr Gängen, die konkurrierend eingelegt sind. Bei zwei Zahnrädern gilt als allgemeine Regel: Wenn das Antriebszahnrad (das Zahnrad, das die Drehkraft direkt vom Motor, Motor usw. erhält) größer als das angetriebene Zahnrad ist, dreht sich das angetriebene Zahnrad schneller und umgekehrt. Wir können dieses Grundkonzept in eine Formel schreiben Übersetzungsverhältnis = T2/T1, T1 ist die Zähnezahl des ersten Zahnrads und T2 ist die Zähnezahl des zweiten Zahnrads.
Schritt
Methode 1 von 2: Berechnung des Übersetzungsverhältnisses in der Zahnradschaltung
Zwei Gänge
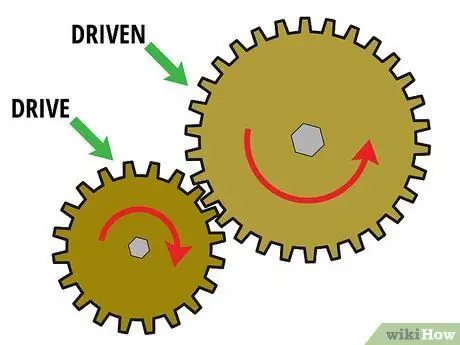
Schritt 1. Beginnen Sie mit einem Satz mit zwei Gängen
Um das Übersetzungsverhältnis zu bestimmen, müssen Sie mindestens zwei Gänge ineinander greifen. Diese beiden ineinandergreifenden Zahnräder werden "Zahnradsätze" genannt. Im Allgemeinen ist das erste Zahnrad ein "Antriebszahnrad", das auf der Motorwelle montiert ist, und das zweite Zahnrad ist ein "Abtriebszahnrad", das auf der Lastwelle montiert ist. Es können auch mehrere Zahnräder dazwischen vorhanden sein, um Kraft vom Antriebszahnrad auf das Abtriebszahnrad zu übertragen. Diese Zahnräder werden "Leerlaufräder" genannt.
Schauen wir uns nun einen Zahnradsatz an, der nur zwei Zahnräder enthält. Um das Übersetzungsverhältnis zu berechnen, müssen diese beiden Zahnräder miteinander interagieren. Mit anderen Worten, die Zähne müssen ineinander greifen und einer muss den anderen drehen. Angenommen, Sie haben ein kleines Antriebszahnrad (Zahnrad 1), das ein größeres Abtriebszahnrad (Zahnrad 2) dreht
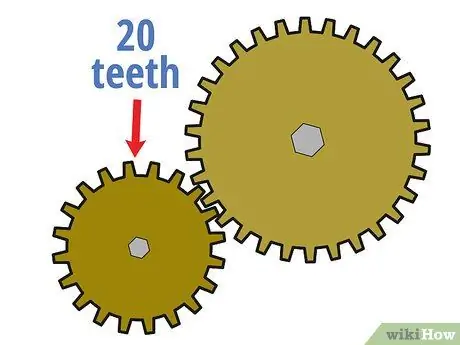
Schritt 2. Zählen Sie die Anzahl der Zähne des Antriebszahnrads
Eine Möglichkeit, das Übersetzungsverhältnis zwischen zwei ineinandergreifenden Zahnrädern zu berechnen, besteht darin, die Anzahl der Zähne (kleine zahnähnliche Erhebungen am Rand des Rades) zu vergleichen, die sie haben. Zählen Sie zunächst, wie viele Zähne das Antriebsrad hat. Sie können dies tun, indem Sie manuell berechnen oder manchmal die auf dem Antriebsrad aufgedruckten Informationen betrachten.
Angenommen, das kleinere Antriebszahnrad im System hat 20 Zähne.
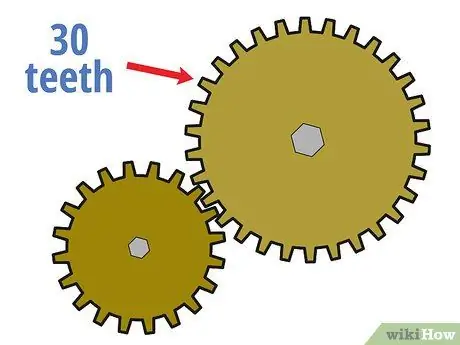
Schritt 3. Zählen Sie die Anzahl der Zähne des angetriebenen Zahnrads
Zählen Sie als nächstes, wie viele Zähne das angetriebene Zahnrad hat, wie Sie es zuvor für das Antriebszahnrad getan haben.
Angenommen, das angetriebene Zahnrad hat 30 Zähne.
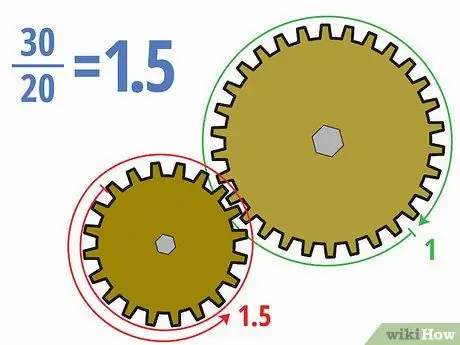
Schritt 4. Teilen Sie die Anzahl der Zähne durcheinander
Da Sie nun wissen, wie viele Zähne jedes Zahnrad hat, können Sie die Übersetzungsverhältnisse ziemlich einfach berechnen. Teilen Sie die Zähne des Abtriebsrads durch die Zähne des Antriebsrads. Sie können die Antwort je nach Ihrer Aufgabe in Dezimal-, Bruch- oder Verhältnisform (wie x: y) schreiben.
- Im obigen Beispiel ergibt die Division von 30 Zähnen im Abtriebsrad durch 20 Zähne im Antriebsrad 30/20 = 1, 5. Wir können es auch schreiben 3/2 oder 1, 5: 1.
- Die Bedeutung dieses Übersetzungsverhältnisses ist, dass sich das kleinere Antriebszahnrad eineinhalb Mal drehen muss, damit das größere angetriebene Zahnrad eine vollständige Umdrehung macht. Da das angetriebene Zahnrad größer ist, dreht sich das angetriebene Zahnrad langsamer.
Mehr als zwei Gänge
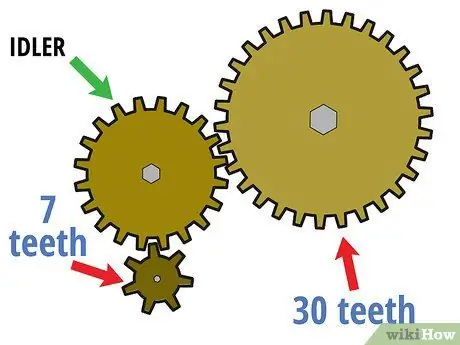
Schritt 1. Beginnen Sie mit einem Zahnradsatz, der mehr als zwei Gänge hat
Wie der Name schon sagt, kann ein "Radsatz" aus einer langen Reihe von Zahnrädern bestehen, nicht nur aus einem Antriebsrad und einem Abtriebsrad. Dabei bleibt der erste Gang das Antriebsrad, der letzte Gang bleibt das Abtriebsrad und der mittlere Gang wird zum "Leerlaufrad". Diese unbelasteten Zahnräder werden oft verwendet, um die Drehrichtung zu ändern oder zwei Zahnräder zu verbinden, wenn eine direkte Gangverstellung sie schwer oder nicht verfügbar machen würde.
Angenommen, die oben beschriebene Zwei-Gang-Schaltung wird nun von einem Zahnrad mit sieben winzigen Zähnen angetrieben. In diesem Fall wurde das Zahnrad mit 30 festen Zähnen zum angetriebenen Zahnrad und das Zahnrad mit 20 Zähnen (das früher der Antrieb war) ist jetzt das unbelastete Zahnrad
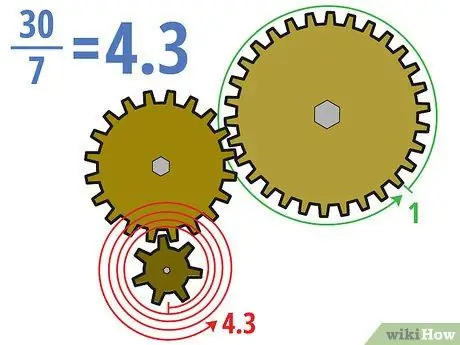
Schritt 2. Teilen Sie die Zähnezahl des Antriebsrads und des Abtriebsrads
Wichtig bei Radsätzen mit mehr als zwei Gängen ist, dass nur das Antriebsrad und das Abtriebsrad (normalerweise der erste und letzte Gang) wichtig sind. Mit anderen Worten, Leerlaufzahnräder haben keinen Einfluss auf das Übersetzungsverhältnis des gesamten Satzes. Nachdem Sie Antriebsrad und Abtriebsrad identifiziert haben, können Sie die Übersetzungen wie zuvor berechnen.
Im obigen Beispiel berechnen wir das Übersetzungsverhältnis, indem wir die dreißig Zähne des Abtriebsrads durch die sieben Zähne des neuen Antriebsrads dividieren. 30/7 = ca. 4, 3 (oder 4, 3: 1). Das bedeutet, dass sich das Antriebsrad etwa 4,3 Mal drehen muss, damit sich das viel größere Abtriebsrad einmal dreht.
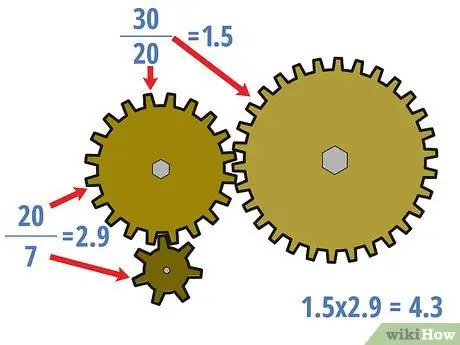
Schritt 3. Berechnen Sie ggf. das Übersetzungsverhältnis für das mittlere Zahnrad
Sie können Übersetzungsverhältnisse berechnen, die auch unbelastete Gänge beinhalten, und dies möchten Sie in bestimmten Situationen tun. Beginnen Sie in diesem Fall beim Antriebszahnrad und arbeiten Sie sich bis zum Lastzahnrad vor. Behandeln Sie den vorherigen Gang bis zum nächsten Gang wie ein Antriebsrad. Dividieren Sie die Zähnezahl jedes "angetriebenen" Zahnrads durch die Anzahl der Zähne des "Antriebszahnrads" für jeden Satz ineinandergreifender Zahnräder, um das mittlere Übersetzungsverhältnis zu berechnen.
- Im obigen Beispiel beträgt das mittlere Übersetzungsverhältnis 20/7 = 2, 9 und 30/20 = 1, 5. Es sollte beachtet werden, dass diese Übersetzungen nicht mit dem Übersetzungsverhältnis für den gesamten Satz übereinstimmen, das 4,3 beträgt.
- jedoch, ist auch zu beachten, dass (20/7) × (30/20) = 4, 3. Im Allgemeinen sollten die Übersetzungen der mittleren Zahnräder des Zahnradsatzes so multipliziert werden, dass sie der Übersetzung aller Zahnräder entsprechen.
Methode 2 von 2: Verhältnis-/Geschwindigkeitsberechnungen durchführen
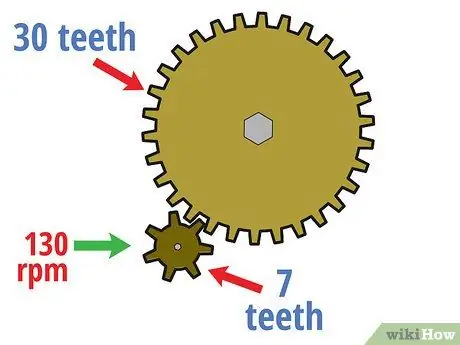
Schritt 1. Berechnen Sie die Drehzahl des Antriebszahnrads
Mit dem Konzept der Übersetzungsverhältnisse lässt sich anhand der „Eingangs“-Drehzahl des Antriebsrads leicht bestimmen, wie schnell sich das Abtriebsrad dreht. Berechnen Sie zunächst die Drehzahl des Antriebsrades. In vielen Getriebeberechnungen ergeben sich daraus Umdrehungen pro Minute (U/min), obwohl auch andere Geschwindigkeitseinheiten verwendet werden können.
Angenommen, im Beispiel der obigen Zahnradschaltung mit einem Antriebszahnrad mit sieben Zähnen und einem Abtriebszahnrad mit 30 Zähnen dreht sich das Antriebszahnrad mit einer Geschwindigkeit von 130 U/min. Mit diesen Informationen berechnen wir in den folgenden Schritten die Drehzahl des Abtriebsrades
Schritt 2. Setzen Sie diese Informationen in die Formel S1 × T1 = S2 × T2 ein
In dieser Formel bezieht sich S1 auf die Drehzahl des Antriebsrads, T1 auf die Zähne des Antriebsrads und S2 und T2 auf die Drehzahl und Zähne des Abtriebsrads. Füllen Sie diese Variablen aus, bis Sie nur noch eine Variable haben.
- In solchen Fragen finden Sie oft die Größe von S2, obwohl es möglich ist, andere Variablen zu finden. Im obigen Beispiel erhalten wir durch Eingabe der uns vorliegenden Informationen:
- 130 U/min × 7 = S2 × 30
Schritt 3. Fertig
Die Berechnung der verbleibenden Variablen ist nur ein grundlegendes mathematisches Problem. Vereinfachen Sie die verbleibenden Gleichungen und isolieren Sie die Variable auf einer Seite des Gleichungszeichens und Sie erhalten die Antwort. Vergiss nicht, es in den richtigen Einheiten zu schreiben. Sie können dadurch an Wert von Hausaufgaben verlieren.
- Im obigen Beispiel können wir dies lösen durch:
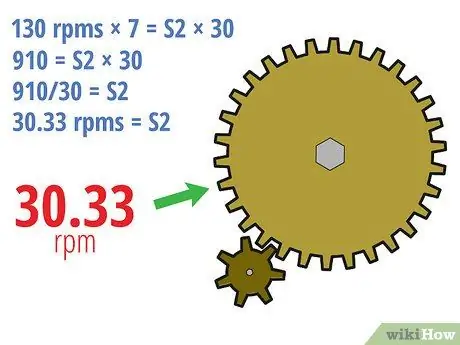
- 130 U/min × 7 = S2 × 30
- 910 = S2 × 30
- 910/30 = S2
- 30, 33 U/min = S2
- Mit anderen Worten, wenn sich das Antriebszahnrad mit einer Geschwindigkeit von 130 U/min dreht, dreht sich das angetriebene Zahnrad mit einer Geschwindigkeit von 30,33 U/min. Da das angetriebene Zahnrad viel größer ist, dreht sich das angetriebene Zahnrad viel langsamer.
Tipps
- Um zu sehen, wie das Übersetzungsverhältnis angewendet wird, versuchen Sie es mit dem Fahrrad. Beachten Sie, dass Sie am einfachsten klettern können, wenn Sie vorne einen kleinen Gang und hinten einen großen Gang haben. Es ist einfacher, den kleineren Gang mit der Kraft der Pedale zu drehen, aber das Hinterrad braucht viele Umdrehungen, verglichen mit der Gangeinstellung, die Sie für ebene Oberflächen verwenden würden. Dadurch bewegen Sie sich langsamer.
- Ein herabgestuftes System (wenn die Lastdrehzahl unter der Motordrehzahl liegt) erfordert einen Motor, der bei höheren Drehzahlen optimale Leistung liefert.
- Die zum Antrieb der Last erforderliche Leistung wird vom Motor über die Übersetzungsverhältnisse angehoben oder abgesenkt. Dieser Motor muss nach Berechnung des Übersetzungsverhältnisses angepasst werden, um die von der Last benötigte Leistung bereitzustellen. Ein angehobenes System (wenn die Lastdrehzahl höher als die Motordrehzahl ist) erfordert einen Motor, der bei niedrigeren Drehzahlen optimale Leistung liefert.






