- Autor Jason Gerald [email protected].
- Public 2024-01-19 22:12.
- Zuletzt bearbeitet 2025-06-01 06:05.
Mathe ist schwer. Selbst die Grundkonzepte vergisst man leicht, wenn man versucht, sich an die vielen verschiedenen Prinzipien und Methoden zu erinnern. Hier sind zwei neue Möglichkeiten, Brüche zu vereinfachen.
Schritt
Methode 1 von 4: Verwenden des größten gemeinsamen Faktors

Schritt 1. Notieren Sie die Zähler- und Nennerfaktoren
Faktoren sind Zahlen, die Sie multiplizieren können, um eine andere Zahl zu erhalten. Zum Beispiel sind 3 und 4 Faktoren von 12, weil Sie sie miteinander multiplizieren können, um 12 zu erhalten. Um die Faktoren einer Zahl aufzuschreiben, müssen Sie nur alle Zahlen aufschreiben, die multipliziert werden können, um diese Zahl zu erhalten, und die teilbar sind durch die Faktoren.
-
Schreiben Sie die Faktoren der Zahl vom kleinsten zum größten auf, ohne den Faktor 1 zu vergessen. So schreiben Sie beispielsweise den Zähler und Nenner des Bruchs 24/32 auf:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

Schritt 2. Finden Sie den größten gemeinsamen Faktor (GCF) von Zähler und Nenner
GCF ist die größte Zahl, die zwei oder mehr Zahlen gleichmäßig teilen kann. Nachdem Sie alle Faktoren der Zahl aufgeschrieben haben, müssen Sie nur noch die größte Zahl finden, die in beiden Faktorenlisten gleich ist.
-
24: 1, 2, 3, 4, 6,
Schritt 8., 12, 24.
-
32: 1, 2, 4,
Schritt 8., 16, 32.
-
Der GCF von 24 und 32 ist 8, weil 8 die größte Zahl ist, die 24 und 32 gleichmäßig teilen kann.

Schritt 3. Dividieren Sie den Zähler und den Bruch durch den GCF
Jetzt, da Sie die GCF haben, müssen Sie nur noch Zähler und Nenner durch diese Zahl dividieren, um Ihren Bruch auf seine einfachste Form zu vereinfachen. So geht's:
- 24/8 = 3
- 32/8 = 4
- Der einfache Bruch ist 3/4.

Schritt 4. Überprüfen Sie Ihre Arbeit
Wenn Sie sicherstellen möchten, dass Sie den Bruch korrekt vereinfacht haben, müssen Sie nur den neuen Zähler und Nenner mit ihrem GCF multiplizieren, um den ursprünglichen Bruch zurückzubekommen. So geht's:
- 3 * 8 = 24
- 4 * 8 = 32
-
Sie sind zu seiner ursprünglichen Form zurückgekehrt, die 24/32 lautet.
Sie können auch den Bruch überprüfen, um sicherzustellen, dass er nicht weiter vereinfacht werden kann. Da 3 eine Primzahl ist, kann sie nur durch 1 und sich selbst geteilt werden, und vier ist nicht durch 3 teilbar, sodass der Bruch nicht weiter vereinfacht werden kann
Methode 2 von 4: Weiter durch kleine Zahlen teilen

Schritt 1. Wählen Sie eine kleine Zahl
Bei dieser Methode müssen Sie zunächst nur eine kleine Zahl auswählen, z. B. 2, 3, 4, 5 oder 7. Schauen Sie sich die Brüche an, um sicherzustellen, dass jeder Teil durch die von Ihnen gewählte Zahl teilbar ist. Wenn Sie beispielsweise einen Bruch von 24/108 haben, wählen Sie nicht 5, da sie nicht durch 5 teilbar sind. Wenn Sie jedoch einen Bruch von 25/60 haben, ist 5 die richtige Zahl.
Für den Bruch 24/32 ist 2 eine gute Zahl. Da beide Zahlen gerade Zahlen sind, sind sie durch 2 teilbar

Schritt 2. Dividiere den Zähler und Nenner des Bruchs durch die Zahl
Der neue Bruch besteht aus einem neuen Zähler und Nenner, die Sie erhalten, nachdem Sie den oberen und unteren Teil des Bruchs 24/32 durch 2 geteilt haben. So geht's:
- 24/2 = 12
- 32/2 = 16
- Dein neuer Bruch ist 12/16.
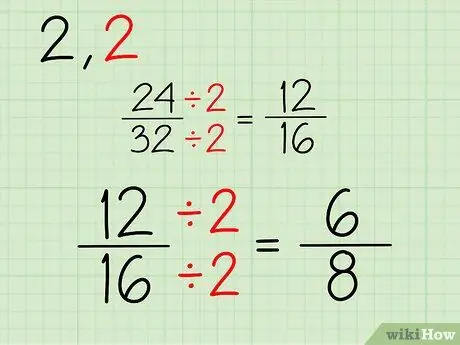
Schritt 3. Wiederholen
Setzen Sie diesen Vorgang fort. Da beide Zahlen gerade Zahlen sind, können Sie weiterhin durch 2 teilen. Wenn einer oder beide Zähler und Nenner ungerade Zahlen sind, können Sie versuchen, durch eine andere Zahl zu teilen. So vereinfachen Sie den 12/16-Bruch:
- 12/2 = 6
- 16/2 = 8
- Ihr neuer Bruch ist 6/8.

Schritt 4. Teilen Sie die Zahl so lange, bis sie nicht mehr teilbar ist
Der neue Zähler und Nenner sind ebenfalls gerade Zahlen, sodass Sie weiterhin durch 2 teilen können. So geht's:
- 6/2 = 3
- 8/2 = 4
- Dein neuer Bruch ist 3/4.

Schritt 5. Stellen Sie sicher, dass der Bruch nicht weiter vereinfacht werden kann
Im Bruch 3/4 ist 3 eine Primzahl, die Faktoren sind also nur 1 und sich selbst, und 4 ist nicht durch 3 teilbar, sodass der Bruch nicht weiter vereinfacht werden kann. Wenn der Zähler oder Nenner des Bruchs nicht mehr durch die von Ihnen ausgewählte Zahl geteilt werden kann, können Sie ihn möglicherweise noch durch eine andere Zahl teilen.
Wenn Sie beispielsweise den Bruch 10/40 haben und Zähler und Nenner durch 5 teilen, ist das Ergebnis 2/8. Sie können den Zähler und den Bruch nicht weiter durch 5 teilen, aber Sie können beide durch 2 teilen, sodass das Endergebnis 1/4 ist

Schritt 6. Überprüfen Sie Ihre Arbeit
Multiplizieren Sie 3/4 mit 2/2 noch einmal dreimal, um sicherzustellen, dass Sie den Anfangsbruch erhalten, der 24/32 ist. So geht's:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- Beachten Sie, dass Sie 24/32 durch 2 * 2 * 2 teilen, was der Division durch 8 entspricht, dem größten GCF von 24 und 32.
Methode 3 von 4: Faktoren schreiben

Schritt 1. Schreiben Sie Ihren Bruch auf
Lassen Sie auf der rechten Seite Ihres Papiers einen großen Platz - Sie benötigen ihn, um die Faktoren aufzuschreiben.

Schritt 2. Notieren Sie die Faktoren von Zähler und Nenner
Allein die Faktoren der beiden. Am einfachsten ist es, die Faktoren übereinander zu schreiben. Beginnen Sie mit der Zahl 1 und schreiben Sie die Faktoren auf.
-
Wenn Ihr Bruch beispielsweise 24/60 beträgt, beginnen Sie mit 24.
Notieren Sie: 24 -- 1, 2, 3, 4, 6, 8, 12, 24
-
Dann die Zahl 60.
Aufschreiben: 60 -- 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Schritt 3. Finden und dividieren Sie durch den größten gemeinsamen Faktor
Dieser Begriff kann in Ihrem gedruckten Buch als GCF geschrieben werden. Was ist die größte Zahl, die Zähler und Nenner teilen kann? Was auch immer die Zahl ist, dividiere beide Zahlen durch diese Zahl.
In unserem Beispiel ist die größte Zahl, die ein Faktor beider Zahlen ist, 12. Wir teilen also 24 durch 12 und 60 durch 12, was uns 2/5 ergibt - unser einfacher Bruch
Methode 4 von 4: Verwenden eines Primfaktorbaums

Schritt 1. Finden Sie die Primfaktoren von Zähler und Nenner
Eine Primzahl ist eine Zahl, die durch keine andere Zahl (außer sich selbst und 1 natürlich) geteilt werden kann. 2, 3, 5, 7 und 11 sind Beispiele für Primzahlen.
- Beginnen Sie mit dem Zähler. Von 24 in 2 und 12 teilen. Da 2 bereits eine Primzahl ist, müssen Sie sie nicht mehr teilen! Dann teile 12 in 2 Zahlen auf: 2 und 6. 2 sind Primzahlen - großartig! Teilen Sie nun 6 in 2 Zahlen: 2 und 3. Sie haben jetzt 2, 2, 2 und 3 als Ihre Primzahlen.
- Arbeite nun am Nenner. Teilen Sie Ihren Baum von 60 in 2 und 30 auf. 30 teilen Sie dann in 2 und 15. Dann teilen Sie 15 in 3 und 5, die beide Primzahlen sind. Jetzt haben Sie 2, 2, 3 und 5 als Primzahlen.
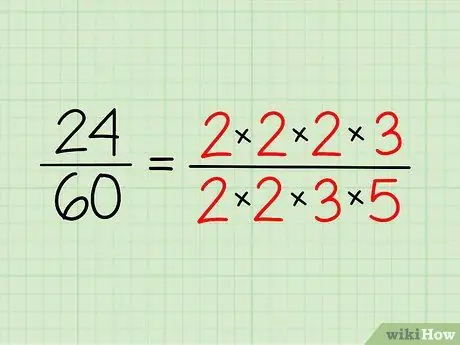
Schritt 2. Schreiben Sie die Primfaktorzerlegung jeder Zahl auf
Schreibe zu jeder Zahl die Primzahlen auf und schreibe sie in Multiplikationsform. Sie müssen es nicht multiplizieren - es ist nur eine Möglichkeit, es leichter zu sehen.
- Für 24 hast du also 2 x 2 x 2 x 3 = 24.
- Für 60 hast du 2 x 2 x 3 x 5 = 60

Schritt 3. Beseitigen Sie die gleichen Faktoren
Jede Zahl, die Teil beider Zahlen ist, kann verworfen werden. In diesem Beispiel sind die gleichen Faktoren ein Paar 2er und eine 3. Auf Wiedersehen!
- Der Rest ist 2 und 5 - oder 2/5! Die gleiche Antwort bekamen wir den Weg oben.
- Wenn Zähler und Nenner des Bruchs gerade Zahlen sind, dividiere nicht einfach durch zwei. Fahren Sie mit der Division fort, bis die Zahl, die Sie erhalten, nicht mehr geteilt werden kann.






