- Autor Jason Gerald [email protected].
- Public 2023-12-16 11:03.
- Zuletzt bearbeitet 2025-01-23 12:15.
Die Quadratwurzel einer Zahl ist leicht zu finden, wenn die Antwort eine ganze Zahl ist. Wenn die Antwort keine ganze Zahl ist, können Sie einer Reihe von Verfahren folgen, um die Quadratwurzel zu erhalten, auch wenn Sie keinen Taschenrechner verwenden. Dazu müssen Sie die Grundlagen der Multiplikation, Addition und Division verstehen.
Schritt
Methode 1 von 3: Finden der Quadratwurzel einer ganzen Zahl
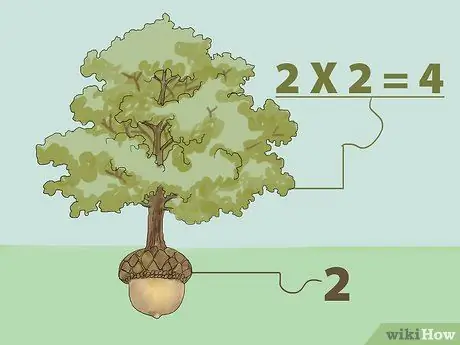
Schritt 1. Finden Sie die perfekte Quadratwurzel durch Multiplizieren
Die Quadratwurzel einer Zahl ist eine Zahl, die, wenn sie mit sich selbst multipliziert wird, die ursprüngliche Zahl zurückgibt. Mit anderen Worten: "Welche Zahl können wir mit sich selbst multiplizieren, um die gewünschte Zahl zu erhalten?"
- Zum Beispiel ist die Quadratwurzel von 1 1, weil 1 multipliziert mit 1 1 ist (1X1=1). Somit ist die Quadratwurzel von 4 2, weil 2 multipliziert mit 2 4 ist (2X2=4). Stellen Sie sich das Quadratwurzelkonzept als Baum vor. Ein Baum wächst aus Samen. Ein Baum ist also größer als ein Samen, der aus einem Samen wächst, der seine Wurzel ist. Aus dem obigen Beispiel ist 4 der Baum und 2 der Samen.
- Die Quadratwurzel von 9 ist also 3 (3X3=9), von 16 ist 4 (4X4=16), von 25 ist 5 (5X5=25), von 36 ist 6 (6X6=36), von 49 ist 7 (7X7 =49), aus 64 ist 8 (8X8=64), aus 81 ist 9 (9X9=81) und aus 100 ist 10 (10X10=100).
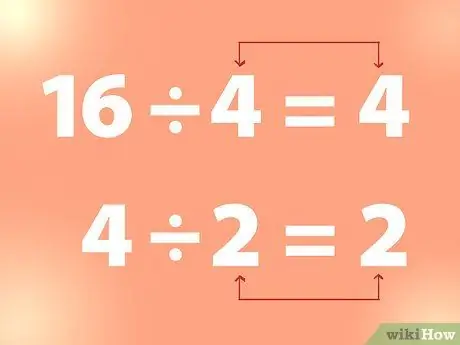
Schritt 2. Verwenden Sie eine kontinuierliche Division, um die Quadratwurzel zu finden
Um die Quadratwurzel einer ganzen Zahl zu finden, können Sie die ganze Zahl durch eine Zahl dividieren, bis Sie eine Zahl erhalten, die dem Teiler entspricht.
- Beispiel: 16 geteilt durch 4 ist 4. Und 4 geteilt durch 2 ist 2, und so weiter. Aus dem obigen Beispiel ist also 4 die Quadratwurzel von 16 und 2 ist die Quadratwurzel von 4.
- Perfekte Quadratwurzeln haben keine Brüche oder Dezimalzahlen, da sie ganze Zahlen sind.
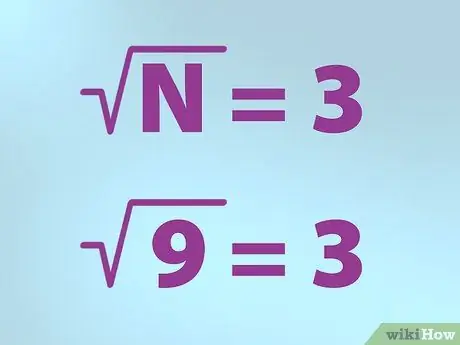
Schritt 3. Verwenden Sie das richtige Symbol für die Quadratwurzel
Mathematiker verwenden ein spezielles Symbol, um die Quadratwurzel darzustellen. Die Form ist wie ein Häkchen mit plus einer Linie oben rechts.
- N ist die Zahl, für die Sie die Quadratwurzel finden möchten. N wird unter das Häkchen gesetzt.
- Wenn Sie also die Quadratwurzel von 9 finden möchten, schreiben Sie eine Formel, indem Sie "N" (9) in ein Häkchen setzen (Symbol "Wurzel"), dann ein Gleichheitszeichen und gefolgt von 3. Es bedeutet "Quadratwurzel von " 9 ist gleich 3".
Methode 2 von 3: Finden der Quadratwurzel einer anderen Zahl
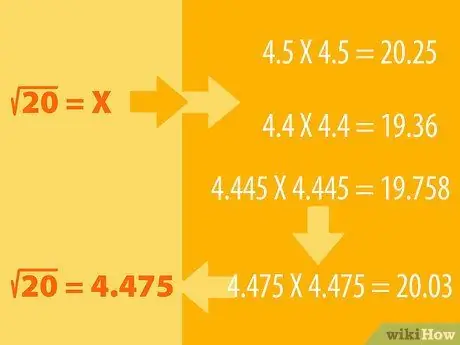
Schritt 1. Raten Sie und führen Sie den Eliminierungsprozess durch
Es ist schwierig, die Quadratwurzel einer nicht ganzzahligen Zahl zu finden. Das heißt jedoch nicht, dass es unmöglich ist.
- Angenommen, Sie möchten die Quadratwurzel von 20 finden. Wir wissen, dass 16 ein perfektes Quadrat ist, dessen Quadratwurzel 4 (4X4=16) ist. Dann sind die 25 Quadratwurzeln 5 (5X5=25), also muss die Quadratwurzel von 20 zwischen den beiden liegen.
- Sie können vermuten, dass die Quadratwurzel von 20 4,5 ist. Quadrat nun 4,5, um das Ergebnis zu sehen. Das heißt, wir multiplizieren 4, 5 mit sich selbst: 4, 5X4, 5. Sehen Sie, ob die Antwort mehr oder weniger als 20 ist. Wenn Ihre Schätzung zu weit ist, versuchen Sie es mit einer anderen Zahl (z. B. 4, 6 oder 4, 4) und passen Sie an raten Sie entsprechend, bis Sie die Zahl 20 erhalten.
- Zum Beispiel 4, 5X4, 5 = 20, 25, also müssen wir logischerweise eine kleinere Zahl finden, vielleicht 4, 4. 4, 4X4, 4 = 19, 36. Die Quadratwurzel von 20 muss also zwischen 4, 5 und 4, 4. Versuchen Sie es mit 4, 445X4, 445. Das Ergebnis ist 19, 758. Das Ergebnis rückt näher. Versuchen Sie es mit anderen Zahlen, bis Sie 4, 475X4, 475 = 20, 03 erhalten. Aufgerundet ergibt diese Zahl 20.

Schritt 2. Verwenden Sie den Mittelungsprozess
Dieser Prozess beginnt auch mit dem Finden der zwei nächsten perfekten Quadrate, die von der Zahl flankiert werden.
- Dann dividiere diese Zahl durch eine der perfekten Quadratwurzeln. Nehmen Sie die Antwort und ermitteln Sie dann den Durchschnitt zwischen dieser Zahl und der Zahl, deren Wurzel Sie finden möchten (Sie können den Durchschnitt ermitteln, indem Sie die beiden zusammenzählen und durch zwei teilen). Dann dividiere die Anfangszahl durch den erhaltenen Durchschnitt. Im letzten Schritt finden Sie den Durchschnitt der Ergebnisse mit dem beim ersten Mal berechneten Durchschnitt.
- Klingt kompliziert? Mit einem Beispiel wäre es einfacher. 10 liegt beispielsweise zwischen den beiden perfekten Quadraten 9 (3X3=9) und 16 (4X4=16). Die Quadratwurzeln beider Zahlen sind 3 und 4. Teilen Sie also 10 durch die erste Zahl 3. Das Ergebnis ist 3, 33. Berechnen Sie nun den Durchschnitt von 3 und 3, 33, indem Sie sie addieren und durch 2 teilen. Das Ergebnis ist 3, 1667 Teilen Sie nun 10 durch 3,1667. Das Ergebnis ist 3,1579. Dann finden Sie den Durchschnitt von 3,1579 und 3,1667, indem Sie sie addieren und durch 2 teilen.
- Überprüfen Sie Ihr Ergebnis, indem Sie die Antwort (in diesem Beispiel 3, 1623) mit sich selbst multiplizieren. Das Ergebnis von 3,1623 multipliziert mit 3,1623 ergibt 10,001.
Methode 3 von 3: Quadrieren negativer Zahlen
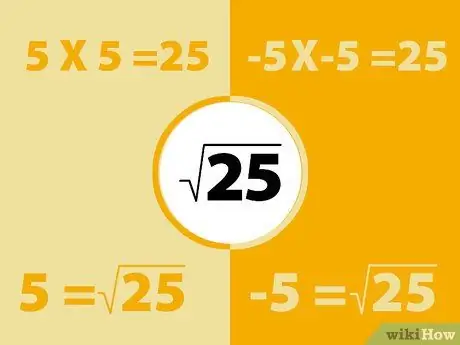
Schritt 1. Quadrieren Sie negative Zahlen mit der gleichen Methode
Denken Sie daran, dass negativ mal negativ positiv ist. Das Quadrat einer negativen Zahl ergibt also eine positive Zahl.
- Zum Beispiel -5X-5 = 25. Denken Sie jedoch auch daran, dass 5x5=25 ist. Die Quadratwurzel von 25 kann also -5 oder 5 sein. Grundsätzlich hat jede Zahl zwei Quadratwurzeln.
- Ähnlich ist 3X3=9 und -3X-3=9, also sind die Quadratwurzeln von 9 3 und -3. Die positive Quadratwurzel wird "Hauptwurzel" genannt. An dieser Stelle müssen wir nur auf diese Antwort achten.
Schritt 2. Verwenden Sie einen Taschenrechner
Während es am besten ist, die Mathematik von Hand zu machen, gibt es viele Online-Rechner zum Berechnen von Quadratwurzeln.
- Suchen Sie auf einem normalen Taschenrechner nach der Quadratwurzel-Schaltfläche.
- Geben Sie im Online-Rechner direkt die Zahl ein, für die Sie die Quadratwurzel ermitteln möchten, und klicken Sie auf die Schaltfläche. Der Computer zeigt Ihnen den Quadratwurzelwert an.
Tipps
-
Behalte immer ein paar wichtige perfekte Quadrate im Hinterkopf:
- 02 = 0, 12 = 1, 32 = 9, 42 = 16, 52 = 25, 62 = 36, 72 = 49, 82 = 64, 92 = 81, 102 = 100,
- Denken Sie auch an dieses perfekte Quadrat: 112 = 121, 122 = 144, 132 169, 142 = 196, 152 = 225, 162 = 256, 172 = 289…
- Beachten Sie auch dies: 102 = 100, 202 = 400, 302 = 900, 402 = 1600, 502 = 2500, …






