- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:12.
- Zuletzt bearbeitet 2025-06-01 06:05.
Die Normalkraft ist die Größe der Kraft, die erforderlich ist, um die anderen Kräfte in einem beliebigen Szenario zu negieren. Der beste Weg, um es zu finden, hängt vom Zustand des Objekts und den vorhandenen Variablen ab. Lesen Sie weiter, um mehr zu erfahren.
Schritt
Methode 1 von 5: Normaler Stil in Ruhe
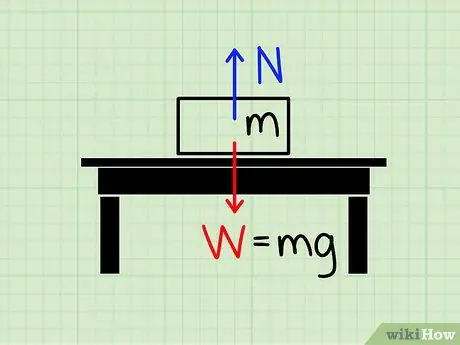
Schritt 1. Verstehen Sie die Bedeutung von Normalkraft
Die Normalkraft bezieht sich auf die Größe der Kraft, die verwendet wird, um die Gravitationskraft zu negieren.
Stellen Sie sich einen ruhenden Block auf einem Tisch vor. Die Schwerkraft zieht den Block in Richtung Erde, aber offensichtlich wirkt eine Kraft, die verhindert, dass der Block den Tisch zerdrückt und zu Boden fällt. Die Kraft, die diesen Block trotz der Schwerkraft stoppt, heißt normaler Stil.
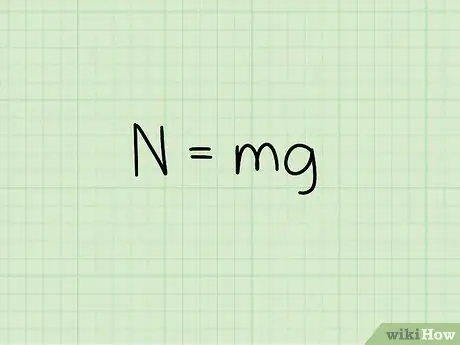
Schritt 2. Kennen Sie die Gleichung für die Normalkraft auf ein ruhendes Objekt
Verwenden Sie zum Berechnen der Normalkraft eines Objekts, wenn es auf einer ebenen Fläche ruht, die Formel: N = m * g
- In dieser Gleichung ist n symbolisiert den normalen Stil, m stellt die Masse des Objekts dar, und g repräsentiert die Erdbeschleunigung.
- Bei einem auf einer ebenen Fläche ruhenden Objekt ohne äußere Krafteinwirkung ist die Normalkraft gleich dem Gewicht des Objekts. Um ein Objekt in Ruhe zu halten, muss die Normalkraft gleich der auf das Objekt wirkenden Gravitationskraft sein. Die auf ein Objekt wirkende Gravitationskraft ist das Gewicht des Objekts oder die Masse des Objekts multipliziert mit der Erdbeschleunigung.
- Beispiel: Bestimmen Sie die Normalkraft eines Blocks mit einer Masse von 4,2 kg.
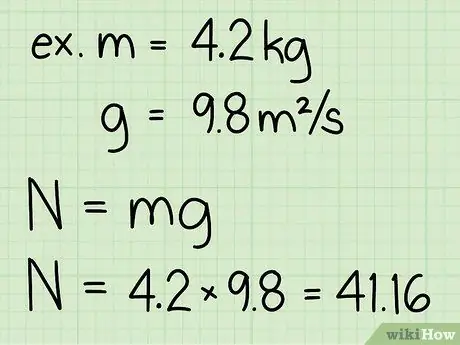
Schritt 3. Multiplizieren Sie die Masse des Objekts und die Erdbeschleunigung
Diese Multiplikation erzeugt das Gewicht des Objekts, das natürlich gleich der Normalkraft des ruhenden Objekts ist.
- Beachten Sie, dass die Erdbeschleunigung auf der Erdoberfläche immer konstant ist: g = 9,8 m/s2
- Beispiel: Gewicht = m * g = 4, 2 * 9, 8 = 41, 16

Schritt 4. Schreiben Sie Ihre Antworten auf
Der vorherige Schritt wird das Problem lösen und Ihnen Ihre Antwort geben.
Beispiel: Die Normalkraft beträgt 41, 16 N
Methode 2 von 5: Normalkraft auf einer schiefen Ebene
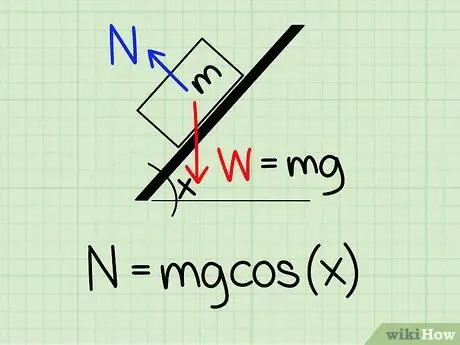
Schritt 1. Verwenden Sie die richtige Gleichung
Um die Normalkraft auf ein um einen bestimmten Winkel geneigtes Objekt zu berechnen, müssen Sie die Formel verwenden: N = m * g * cos(x)
- Für diese Gleichung gilt n symbolisiert den normalen Stil, m repräsentiert die Masse des Objekts g die Erdbeschleunigung darstellt und x stellt den schiefen Winkel dar.
- Beispiel: Bestimmen Sie die Normalkraft eines Blocks mit einer Masse von 4,2 kg, der auf einer schiefen Ebene mit einer Neigung von 45 Grad ruht.

Schritt 2. Bestimmen Sie den Kosinus des Winkels
Der Kosinus des Winkels ist gleich dem Sinus des komplementären Winkels oder der angrenzenden Seite geteilt durch die Hypotenuse des durch die Steigung gebildeten Dreiecks.
- Dieser Wert wird oft mit einem Taschenrechner ermittelt, da der Kosinus jedes Winkels immer konstant ist, Sie können ihn aber auch manuell berechnen.
- Beispiel: cos(45) = 0,71
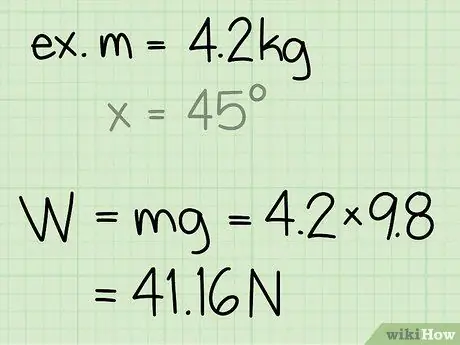
Schritt 3. Finden Sie das Gewicht des Objekts
Das Gewicht eines Objekts ist gleich der Masse des Objekts mal der Erdbeschleunigung.
- Beachten Sie, dass die Erdbeschleunigung auf der Erdoberfläche immer konstant ist: g = 9,8 m/s2
- Beispiel: Gewicht = m * g = 4, 2 * 9, 8 = 41, 16
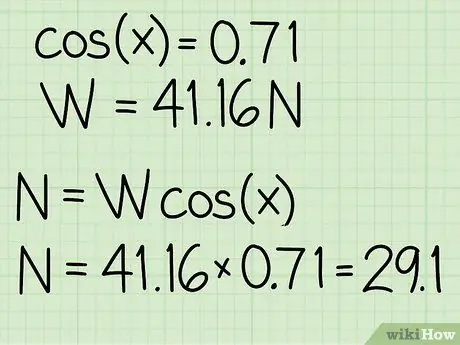
Schritt 4. Multiplizieren Sie die beiden Werte
Um die Normalkraft zu ermitteln, müssen Sie das Gewicht des Objekts mit dem Kosinus des Neigungswinkels multiplizieren.
Beispiel: N = m * g * cos(x) = 41, 16 * 0, 71 = 29, 1
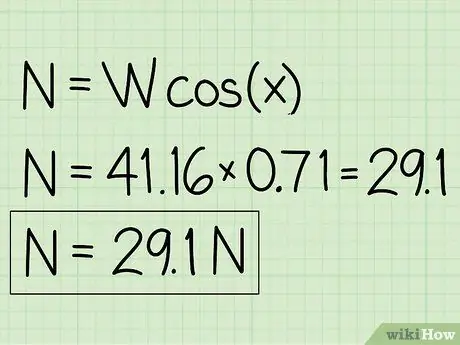
Schritt 5. Schreiben Sie Ihre Antworten auf
Der vorherige Schritt wird das Problem lösen und Ihre Antwort bereitstellen.
- Beachten Sie, dass die Normalkraft geringer ist als das Gewicht des Objekts, wenn ein Objekt auf einer Steigung ruht.
- Beispiel: Die Normalkraft beträgt 29,1 N.
Methode 3 von 5: Normaler Stil mit Outer Down Style
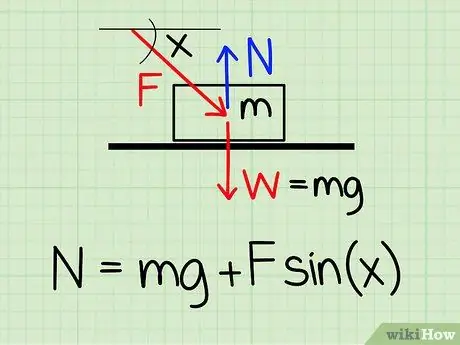
Schritt 1. Verwenden Sie die richtige Gleichung
Um die Normalkraft auf ein ruhendes Objekt zu berechnen, wenn eine externe nach unten gerichtete Kraft auf das Objekt einwirkt, verwenden Sie die Gleichung: N = m * g + F * sin(x)'
- n symbolisiert den normalen Stil, m repräsentiert die Masse des Objekts g stellt die Erdbeschleunigung dar, F symbolisiert den äußeren Stil und x stellt den Winkel zwischen dem Objekt und der Richtung der äußeren Kraft dar.
- Beispiel: Bestimmen Sie die Normalkraft eines Objekts mit einer Masse von 4,2 kg, wenn das Objekt von einer Person in einem Winkel von 30 Grad und einer Kraft von 20,9 N gestoßen wird.
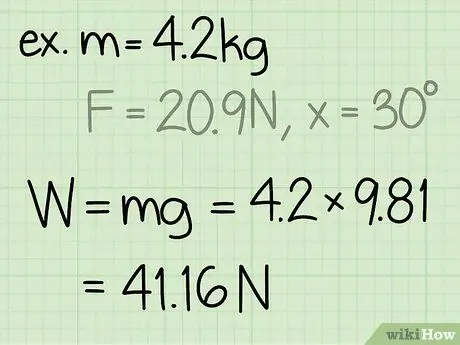
Schritt 2. Finden Sie das Gewicht des Objekts
Das Gewicht eines Objekts ist gleich der Masse des Objekts mal der Erdbeschleunigung.
- Beachten Sie, dass die Erdbeschleunigung auf der Erdoberfläche immer konstant ist: g = 9,8 m/s2
- Beispiel: Gewicht = m * g = 4, 2 * 9, 8 = 41, 16
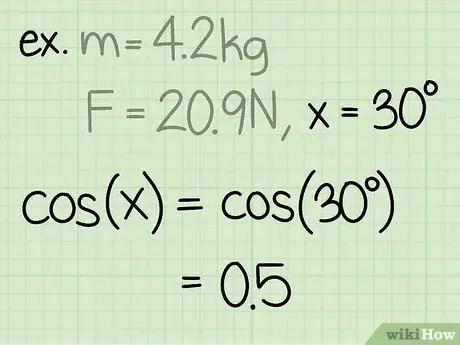
Schritt 3. Finden Sie den Sinus des Winkels
Der Sinus eines Winkels wird berechnet, indem die dem Winkel gegenüberliegende Seite des Dreiecks durch die Hypotenuse des Winkels geteilt wird.
Beispiel: sin(30) = 0,5

Schritt 4. Multiplizieren Sie den Sinus mit der externen Kraft
Externe Kraft bezieht sich in diesem Beispiel auf die nach unten gerichtete Kraft, die auf das Objekt trifft.
Beispiel: 0, 5 * 20, 9 = 10, 45
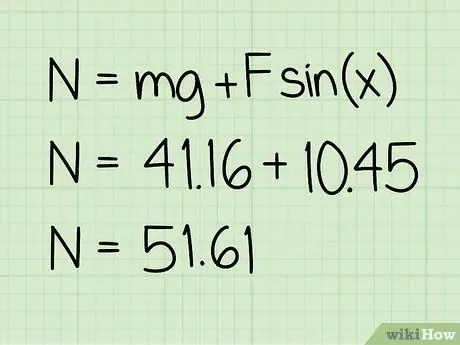
Schritt 5. Addieren Sie diesen Wert zum Gewicht
Diese Summe ergibt die Größe der wirkenden Normalkraft.
Beispiel: 10, 45 + 41, 16 = 51, 61
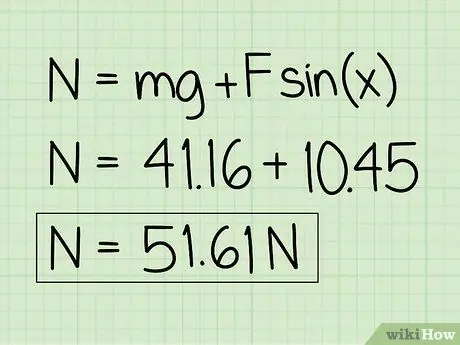
Schritt 6. Schreiben Sie Ihre Antworten auf
Beachten Sie, dass bei einem ruhenden Objekt, das von einer externen Abwärtskraft beeinflusst wird, die Normalkraft größer ist als das Gewicht des Objekts.
Beispiel: Die Normalkraft beträgt 51,61 N
Methode 4 von 5: Normaler Stil mit äußerem Stil nach oben
Schritt 1. Verwenden Sie die richtige Gleichung
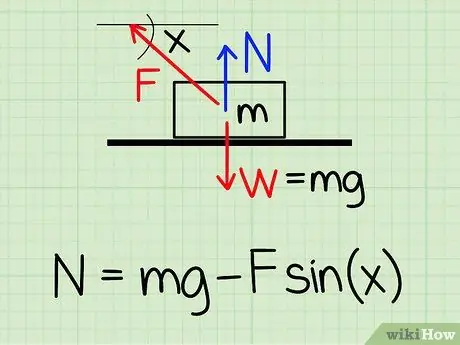
Um die Normalkraft auf ein ruhendes Objekt zu berechnen, wenn eine externe nach oben gerichtete Kraft auf das Objekt einwirkt, verwenden Sie die Gleichung: N = m * g - F * sin(x)'
- n symbolisiert den normalen Stil, m repräsentiert die Masse des Objekts g stellt die Erdbeschleunigung dar, F symbolisiert den äußeren Stil und x stellt den Winkel zwischen dem Objekt und der Richtung der äußeren Kraft dar.
- Beispiel: Bestimmen Sie die Normalkraft eines Blocks mit einer Masse von 4,2 kg, wenn jemand den Block in einem Winkel von 50 Grad und einer Kraft von 20,9 N nach oben zieht.

Schritt 2. Finden Sie das Gewicht des Objekts
Das Gewicht eines Objekts ist gleich der Masse des Objekts mal der Erdbeschleunigung.
- Beachten Sie, dass die Erdbeschleunigung auf der Erdoberfläche immer konstant ist: g = 9,8 m/s2
- Beispiel: Gewicht = m * g = 4, 2 * 9, 8 = 41, 16
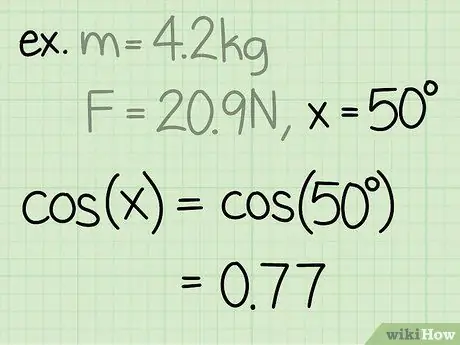
Schritt 3. Finden Sie den Sinus des Winkels
Der Sinus eines Winkels wird berechnet, indem die dem Winkel gegenüberliegende Seite des Dreiecks durch die Hypotenuse des Winkels geteilt wird.
Beispiel: sin(50) = 0, 77

Schritt 4. Multiplizieren Sie den Sinus mit der externen Kraft
Externe Kraft bezieht sich in diesem Fall auf die nach oben gerichtete Kraft, die auf das Objekt trifft.
Beispiel: 0,77 * 20, 9 = 16, 01
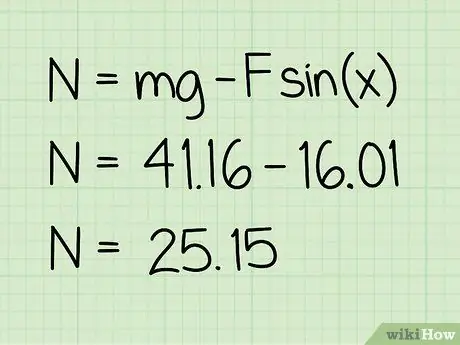
Schritt 5. Ziehen Sie diesen Wert vom Gewicht ab
Durch die Subtraktion erhalten Sie die Größe der Normalkraft, die darauf einwirkt.
Beispiel: 41, 16 - 16, 01 = 25, 15
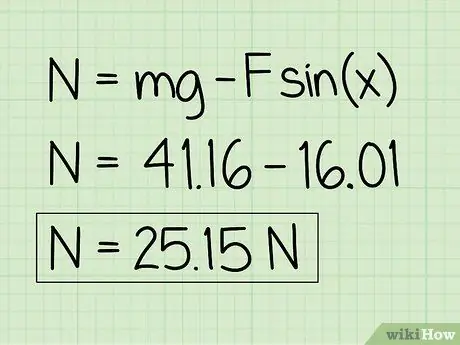
Schritt 6. Schreiben Sie Ihre Antworten auf
Beachten Sie, dass ein ruhendes Objekt von einer aufwärts gerichteten externen Kraft beeinflusst wird, die Normalkraft ist geringer als das Gewicht des Objekts.
Beispiel: Die Normalkraft beträgt 25, 15 N
Methode 5 von 5: Normalkraft und Reibung

Schritt 1. Kennen Sie die Grundgleichung für Gleitreibung
Die kinetische Reibung oder Reibung eines sich bewegenden Objekts ist gleich dem Reibungskoeffizienten mal der Normalkraft eines Objekts. In Gleichungsform: f = * N
- In dieser Gleichung ist F symbolisieren Reibung, ️ den Reibungskoeffizienten darstellt und n stellt die Normalkraft des Objekts dar.
- Der "Reibungskoeffizient" ist das Verhältnis der Reibungskraft zur Normalkraft, die zwei gegenüberliegende Flächen zusammendrückt.
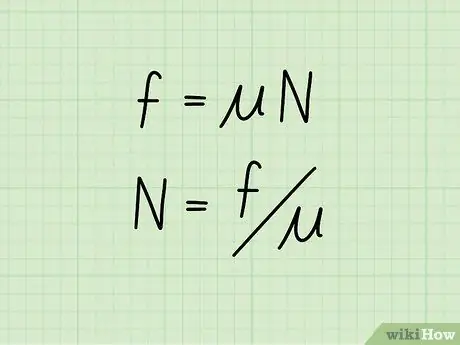
Schritt 2. Stellen Sie die Gleichung auf, um die Normalkraft zu isolieren
Wenn Sie den Wert der Gleitreibung eines Objekts sowie seinen Reibungskoeffizienten kennen, können Sie die Normalkraft mit der Formel berechnen: N = f /
- Beide Seiten der ursprünglichen Gleichung werden geteilt durch ️, wodurch auf der einen Seite die Normalkraft isoliert und auf der anderen der Reibungskoeffizient und die Gleitreibung berechnet werden.
- Beispiel: Bestimmen Sie die Normalkraft eines Blocks, wenn der Reibungskoeffizient 0,4 und die Gleitreibungsgröße 40 N beträgt.
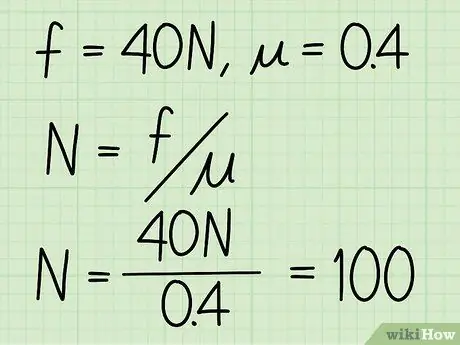
Schritt 3. Teilen Sie die Gleitreibung durch den Reibungskoeffizienten
Im Grunde ist dies alles, was Sie tun müssen, um die Größe der Normalkraft zu bestimmen.
Beispiel: N = f / = 40 / 0, 4 = 100
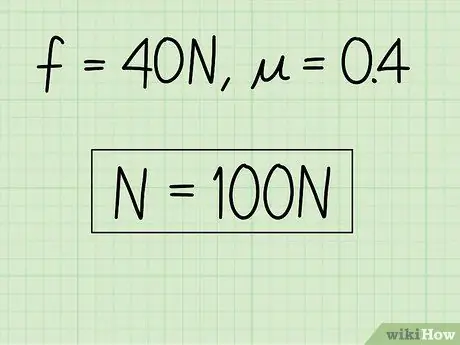
Schritt 4. Schreiben Sie Ihre Antworten auf
Falls gewünscht, können Sie Ihre Antwort überprüfen, indem Sie sie wieder in die ursprüngliche Gleichung für Gleitreibung einsetzen. Wenn Sie es nicht wollen, haben Sie das Problem gelöst.






