Mathe lernen (mit Bildern)

2024 Autor: Jason Gerald | [email protected]. Zuletzt bearbeitet: 2024-02-01 14:12

Jeder kann Mathe lernen, egal ob er bereits auf einer höheren Schulstufe ist oder einfach nur die Grundlagen noch einmal perfektionieren möchte. Nachdem wir besprochen haben, wie man ein guter Mathematiker wird, wird dieser Artikel Ihnen die grundlegenden mathematischen Fortschritte beibringen und Ihnen die grundlegenden Elemente vermitteln, die Sie in jeder Übung lernen müssen. Anschließend werden in diesem Artikel die Grundlagen des Rechnenlernens erörtert, die sowohl Grundschulkindern als auch allen helfen, die die Grundlagen dieses Wissenschaftsbereichs erlernen möchten.

Schritt

Teil 1 von 6: Schlüssel, um ein guter Mathematikstudent zu werden

Schritt 1. Erscheinen Sie in der Klasse

Wenn Sie den Unterricht verpassen, sollten Sie Konzepte von Mitschülern oder aus Ihrem Lehrbuch lernen. Sie werden nie eine Textzusammenfassung von einem Freund so oft bekommen wie von Ihrem Lehrer.

Erscheinen Sie pünktlich zur Klasse. Kommen Sie stattdessen etwas früher und öffnen Sie Ihr Notizbuch an der richtigen Stelle, öffnen Sie Ihr Lehrbuch und nehmen Sie Ihren Taschenrechner heraus, damit Sie bereit sind, loszulegen, wenn Ihr Lehrer bereit ist zu unterrichten.
Nur schwänzen, wenn Sie krank sind. Wenn du den Unterricht wirklich versäumst, bitte deine Mitschüler, herauszufinden, worüber der Lehrer gesprochen hat und welche Hausaufgaben gegeben wurden.

Schritt 2. Arbeiten Sie mit Ihrem Lehrer zusammen

Wenn Ihr Lehrer vor der Klasse an einem Problem arbeitet, arbeiten Sie mit dem Lehrer zusammen, indem Sie das Problem in Ihrem Notizbuch bearbeiten.

Stellen Sie sicher, dass Ihre Notizen klar und leicht zu lesen sind. Schreiben Sie nicht nur Fragen. Schreiben Sie auch alles auf, was der Lehrer sagt, das Ihr Verständnis der erklärten Konzepte verbessern kann.
Vervollständigen Sie die Beispielfragen Ihres Lehrers. Beantworten Sie die gestellten Fragen, während der Lehrer während der Arbeit durch die Klasse geht.
Nehmen Sie teil, wenn der Lehrer ein Problem löst. Warten Sie nicht, bis der Lehrer Sie anruft. Bieten Sie an zu antworten, wenn Sie die Antwort kennen, und heben Sie die Hand, um eine Frage zu stellen, wenn Sie sich über den Lehrstoff nicht sicher sind.

Schritt 3. Machen Sie Ihre Hausaufgaben am selben Tag, an dem Sie Ihre Hausaufgaben aufgeben

Wenn Sie Ihre Hausaufgaben noch am selben Tag machen, ist Ihnen das Konzept noch frisch im Kopf. Manchmal ist es nicht möglich, die Hausaufgaben am selben Tag zu erledigen. Stellen Sie sicher, dass Ihre Hausaufgaben gemacht sind, bevor Sie zum Unterricht gehen.

Schritt 4. Arbeiten Sie außerhalb des Unterrichts, wenn Sie Hilfe benötigen

Besuchen Sie Ihren Lehrer in den Pausen oder während der Sprechzeiten.

Wenn Sie ein Math Center an Ihrer Schule haben, informieren Sie sich über die Öffnungszeiten und bitten Sie um Hilfe.
Treten Sie einer Lerngruppe bei. Eine gute Lerngruppe besteht im Allgemeinen aus 4 oder 5 Personen mit unterschiedlichen Fähigkeiten. Wenn Sie ein C-Student in Mathematik sind, schließen Sie sich einer Gruppe von 2 oder 3 Schülern mit der Note „A“oder „B“an, damit Sie Ihre Fähigkeiten verbessern können. Vermeiden Sie es, sich einer Gruppe von Schülern anzuschließen, deren Noten niedriger sind als Ihre.

Teil 2 von 6: Mathematik lernen in der Schule

Schritt 1. Beginnen Sie mit der Arithmetik

In den meisten Schulen lernen die Schüler in der Grundschule Rechnen. Die Arithmetik umfasst die Grundlagen der Addition, Subtraktion, Multiplikation und Division.

Üben Sie Fragen. Rechenaufgaben immer wieder zu lösen ist der beste Weg, sich die Grundlagen richtig zu merken. Suchen Sie nach Software, mit der Sie eine Vielzahl verschiedener mathematischer Probleme bearbeiten können. Suchen Sie auch nach Problemen mit Zeitrahmen, um Ihre Geschwindigkeit zu verbessern.
Sie können auch online Rechenaufgaben finden und Rechen-Apps auf Ihr Mobilgerät herunterladen.

Schritt 2. Fahren Sie mit der Präalgebra fort

Diese Übung vermittelt Ihnen die Grundelemente, die Sie später benötigen, um algebraische Probleme zu lösen.

Erfahren Sie mehr über Brüche und Dezimalzahlen. Sie lernen, Brüche und Dezimalzahlen zu addieren, zu subtrahieren, zu multiplizieren und zu dividieren. In Bezug auf Brüche lernen Sie, wie man Brüche subtrahiert und kombinierte Zahlen übersetzt. In Bezug auf Dezimalzahlen werden Sie Stellenwerte verstehen und Dezimalzahlen in Story-Aufgaben verwenden können.
Erfahren Sie mehr über Verhältnisse, Proportionen und Prozentsätze. Diese Konzepte helfen Ihnen, Vergleiche anzustellen.
Machen Sie sich mit der grundlegenden Geometrie vertraut. Sie lernen 3D-Formen und -Konzepte kennen. Außerdem lernen Sie Konzepte wie Fläche, Umfang, Volumen und Oberfläche sowie Informationen zu parallelen und senkrechten Linien und Winkeln kennen.
Verstehen Sie einige grundlegende Statistiken. In der Präalgebra umfasst Ihre Einführung in die Statistik im Allgemeinen visuelle Elemente wie Grafiken, Streudiagramme, Stempeldiagramme und Histogramme.
Lernen Sie die Grundlagen der Algebra. Dazu gehören Konzepte wie das Lösen einfacher Gleichungen, die Variablen enthalten, das Erlernen von Eigenschaften wie die Verteilungseigenschaft, das Zeichnen einfacher Gleichungen und das Lösen von Ungleichungen.

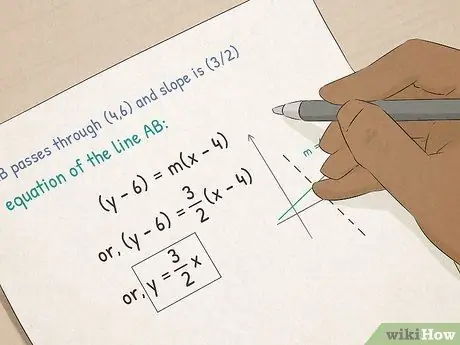
Schritt 3. Gehen Sie zu Algebra I

In Ihrem ersten Jahr der Algebra lernen Sie die grundlegenden Symbole der Algebra kennen. Sie werden auch lernen:

Lösen Sie Gleichungen und Ungleichungen, die Variablen enthalten. Sie lernen, diese Probleme auf Papier und mit Bildern zu lösen.
Lösen Sie Story-Probleme. Sie werden überrascht sein, mit wie vielen alltäglichen Problemen Sie in Zukunft konfrontiert werden, die die Fähigkeit zum Lösen von algebraischen Geschichtenproblemen erfordern. Zum Beispiel würden Sie Algebra verwenden, um den Zinssatz zu ermitteln, den Sie auf Ihrem Bankkonto oder Ihrer Anlage verdienen. Sie können auch Algebra verwenden, um herauszufinden, wie lange Sie basierend auf der Geschwindigkeit Ihres Autos fahren sollten.
Arbeiten Sie mit Exponenten. Wenn Sie mit dem Lösen von Polynomgleichungen (Ausdrücken, die Zahlen und Variablen enthalten) beginnen, werden Sie wissen, wie Exponenten verwendet werden. Dazu gehören wahrscheinlich Übungen mit wissenschaftlicher Notation. Sobald Sie Exponenten beherrschen, können Sie lernen, Polynomausdrücke zu addieren, zu subtrahieren, zu multiplizieren und zu dividieren.
Lösen Sie Quadrat- und Quadratwurzelprobleme. Wenn Sie dieses Thema beherrschen, können Sie sich die Quadrate vieler Zahlen merken. Sie können auch mit Gleichungen arbeiten, die Quadratwurzeln haben.
Funktionen und Graphen verstehen. In der Algebra lernen Sie grafische Gleichungen kennen. Sie erfahren, wie Sie die Steigung einer Linie berechnen, eine Gleichung in Punkt-Neigungs-Form aufstellen und wie Sie den x- und y-Schnitt einer Linie mit der Steigungs-Schnittpunkt-Form berechnen.
Finden Sie das Gleichungssystem heraus. Manchmal bekommt man 2 verschiedene Gleichungen mit den Variablen x und y, und man muss für beide Gleichungen nach x oder y auflösen. Glücklicherweise lernen Sie viele Tricks zum Lösen dieser Gleichungen, einschließlich grafischer Darstellung, Substitution und Addition.

Schritt 4. Geometrie studieren

In der Geometrie lernen Sie die Eigenschaften von Linien, Segmenten, Winkeln und Formen kennen.

Sie werden eine Reihe von Sätzen und Folgerungen auswendig lernen, die Ihnen helfen, die Regeln der Geometrie zu verstehen.
Sie lernen, die Fläche eines Kreises zu berechnen, den Satz des Pythagoras anzuwenden und die Beziehung zwischen den Winkeln und Seiten eines speziellen Dreiecks zu finden.
In zukünftigen standardisierten Tests wie dem SAT, ACT und GRE werden Sie viele Geometriefragen sehen.

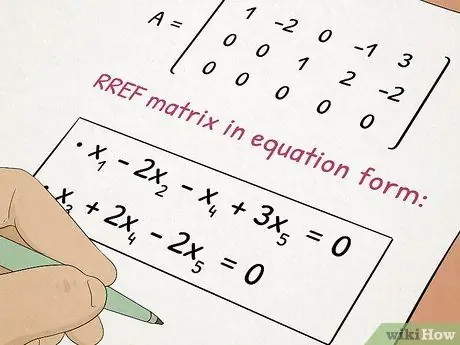
Schritt 5. Nehmen Sie am Algebra II-Kurs teil

Algebra II baut auf den Konzepten auf, die Sie in Algebra I gelernt haben, und ergänzt komplexe Themen wie quadratische Gleichungen und Matrizen.

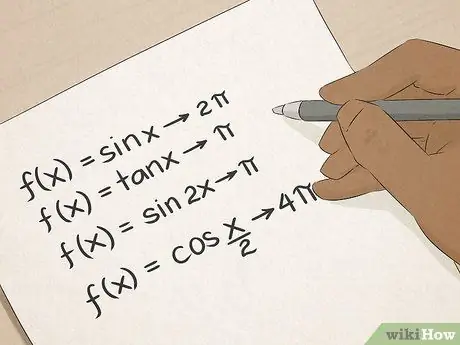
Schritt 6. Meistere die Trigonometrie

Sie kennen trigonometrische Begriffe: Sinus, Cosinus, Tangens und so weiter. Trigonometrie wird Ihnen viele praktische Möglichkeiten zur Berechnung von Winkeln und Linienlängen beibringen, und diese Fähigkeiten werden für Menschen, die im Bauwesen, in der Architektur, im Ingenieurwesen oder im Vermessungswesen tätig sind, von unschätzbarem Wert sein.

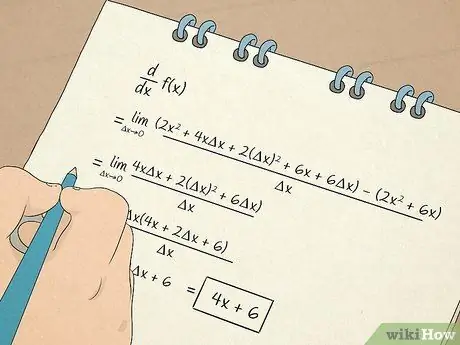
Schritt 7. Führen Sie Kalkülberechnungen durch

Infinitesimalrechnung mag einschüchternd klingen, aber sie ist ein wunderbares Werkzeug, um entweder das Verhalten von Zahlen oder die Welt um Sie herum zu verstehen.

Infinitesimalrechnung wird Ihnen Funktionen und Grenzen beibringen. Sie sehen das Zahlenverhalten von nützlichen Funktionen, einschließlich e^x und logarithmischen Funktionen.
Außerdem lernen Sie das Berechnen und Arbeiten mit Derivaten. Die erste Ableitung gibt Ihnen Informationen basierend auf der Steigung der Tangente an eine Gleichung. Ein Derivat gibt Ihnen beispielsweise die Geschwindigkeit an, mit der sich etwas in einer nichtlinearen Situation ändert. Die zweite Ableitung sagt Ihnen, ob die Funktion über ein bestimmtes Intervall zu- oder abnimmt, damit Sie die Konkavität einer Funktion bestimmen können.
Integrale werden Ihnen beibringen, die Fläche unter einer Kurve sowie ihr Volumen zu berechnen.
Calculus in der High School endet im Allgemeinen in Sequenzen und Sequenzen. Obwohl die Studenten nicht viele Anwendungen für Schaltungen sehen werden, sind Schaltungen wichtig für diejenigen, die Differentialgleichungen studieren.

Teil 3 von 6: Mathematische Grundlagen – Master-Addition

Schritt 1. Beginnen Sie mit "+1"-Fakten

Wenn Sie einer Zahl 1 hinzufügen, gelangen Sie zur höchsten Zahl auf der Zahlengeraden. Zum Beispiel 2 + 1 = 3.

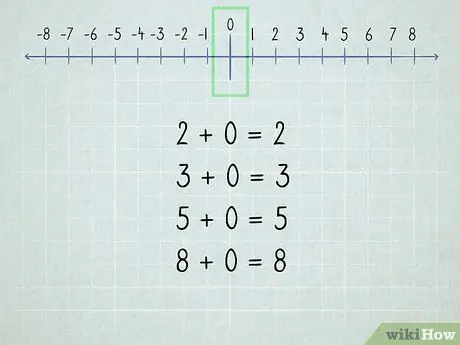
Schritt 2. Verstehen Sie die Null

Alle Zahlen, die zu Null hinzugefügt werden, sind dieselbe Zahl, da "Null" "keine" bedeutet.

Schritt 3. Lernen Sie Doppelzahlen

Mehrere Zahlen sind ein Problem, bei dem zwei gleiche Zahlen addiert werden. 3 + 3 = 6 ist beispielsweise ein Beispiel für eine Gleichung mit mehreren Zahlen.

Schritt 4. Verwenden Sie das Mapping, um mehr über andere Additionslösungen zu erfahren

Im folgenden Beispiel lernen Sie, indem Sie abbilden, was passiert, wenn Sie 3 zu 5, 2 und 1 addieren. Probieren Sie das Problem "Add by 2" selbst aus.

Schritt 5. Fahren Sie fort, bis die Zahl mehr als 10 beträgt

Lernen Sie, 3 Zahlen zu addieren, um eine Zahl größer als 10 zu erhalten.

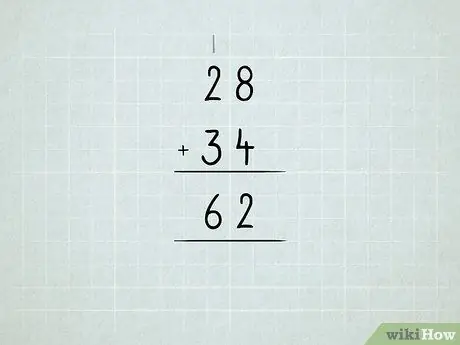
Schritt 6. Addieren Sie die größeren Zahlen

Erfahren Sie, wie Sie Einheiten in Zehner, Zehner in Hunderter usw. umgruppieren.

Addiere zuerst die Zahlen in der rechten Spalte. 8 + 4 = 12, was bedeutet, dass Sie 1 Zahl 10 und 2 Zahl 1 haben. Schreiben Sie die Zahl 2 in die Einheitenspalte.
Schreiben Sie die Zahl 1 in die Zehnerspalte.
Addiere die Zehnerspalte vollständig.

Teil 4 von 6: Mathematische Grundlagen – Reduktionsstrategien

Schritt 1. Beginnen Sie mit „1 Ziffer rückwärts

Wenn Sie 1 von einer Zahl subtrahieren, erhalten Sie 1 Zahl zurück. Zum Beispiel 4 - 1 = 3.

Schritt 2. Lernen Sie, doppelte Zahlen zu subtrahieren

Zum Beispiel addieren Sie die Zahlen 5 + 5, um 10 zu erhalten. Schreiben Sie die Gleichung einfach rückwärts, um 10 - 5 = 5 zu erhalten.

Wenn 5 + 5 = 10, dann 10 - 5 = 5.
Wenn 2 + 2 = 4, dann 4 - 2 = 2.

Schritt 3. Merken Sie sich die Faktenfamilie

Als Beispiel:

3 + 1 = 4
1 + 3 = 4
4 - 1 = 3
4 - 3 = 1

Schritt 4. Finden Sie die fehlenden Zahlen

Beispiel: _ + 1 = 6 (die Antwort ist 5).

Schritt 5. Merken Sie sich die Tatsache der Subtraktion auf 20

Schritt 6. Üben Sie das Subtrahieren von 1-stelligen Zahlen von 2-stelligen Zahlen ohne Ausleihen

Subtrahiere die Zahlen in der Einer-Spalte und verkleinere die Zahlen in der Zehner-Spalte.

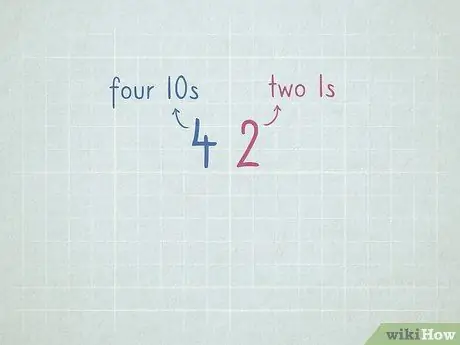
Schritt 7. Üben Sie den Stellenwert, um sich auf das Subtrahieren durch Anleihen vorzubereiten

32 = 3 Zahlen 10 und 2 Zahlen 1.
64 = 6 Zahlen 10 und 4 Zahlen 1.
96 = _ Nummer 10 und _ Nummer 1.

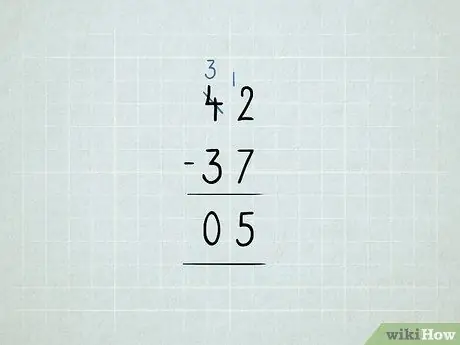
Schritt 8. Subtrahieren Sie durch Ausleihen

Sie möchten 42 - 37 subtrahieren. Sie beginnen damit, 2 - 7 in der Einheitenspalte zu subtrahieren. Es stellte sich heraus, dass es nicht funktionierte!
Leihen Sie sich die Zahl 10 aus der Zehnerspalte und setzen Sie sie in die Einerspalte. Jetzt hast du 3 10er statt 4 10er Jetzt hast du 12 1er statt 2 1er.
Ziehen Sie zuerst Ihre Einheitenspalte ab: 12 - 7 = 5. Überprüfen Sie dann die Zehnerspalte. Da 3 - 3 = 0 ist, müssen Sie die Zahl 0 nicht aufschreiben. Ihre Antwort ist 5.

Teil 5 von 6: Mathematische Grundlagen – Master-Multiplikation

Schritt 1. Beginnen Sie mit der Zahl 1 und der Zahl 0

Alle Zahlen, die mit 1 multipliziert werden, sind gleich der Zahl selbst. Jede mit 0 multiplizierte Zahl ist gleich Null.

Schritt 2. Merken Sie sich das Einmaleins

Schritt 3. Üben Sie mit einstelligen Multiplikationsaufgaben

Schritt 4. Multiplizieren Sie die 2-stellige Zahl mit der 1-stelligen Zahl

Multiplizieren Sie die untere rechte Zahl mit der oberen rechten Zahl.
Multiplizieren Sie die untere rechte Zahl mit der oberen linken Zahl.

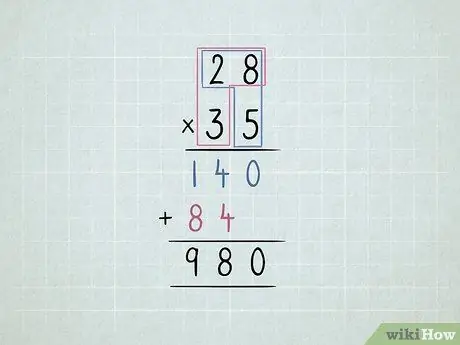
Schritt 5. Multiplizieren Sie 2 2-stellige Zahlen

Multiplizieren Sie die untere rechte Zahl mit der oberen rechten Zahl und dann mit der oberen linken Zahl.
Verschieben Sie die zweite Zeile um eine Ziffer nach links.
Multiplizieren Sie die untere linke Zahl mit der oberen rechten Zahl und dann die obere linke Zahl.
Addiere alle Spalten.

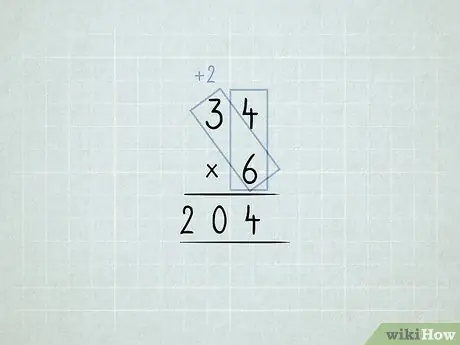
Schritt 6. Multiplizieren Sie die Spalten und gruppieren Sie sie neu

Sie möchten 34 x 6 multiplizieren. Sie beginnen damit, die Einheitenspalte (4 x 6) zu multiplizieren, aber Sie können nicht 24 1s in der Einerspalte haben.
Speichern Sie 4 1s in der Einheitenspalte. Verschiebe 2 10s in die Zehnerspalte.
Multiplizieren Sie 6 x 3, was 18 ergibt. Addieren Sie die 2, die Sie verschoben haben, was 20 entspricht.

Teil 6 von 6: Mathematische Grundlagen – Divisionsprobleme aufdecken

Schritt 1. Denken Sie an die Division im Gegensatz zur Multiplikation

#* Wenn 4 x 4 = 16, dann 16 / 4 = 4.

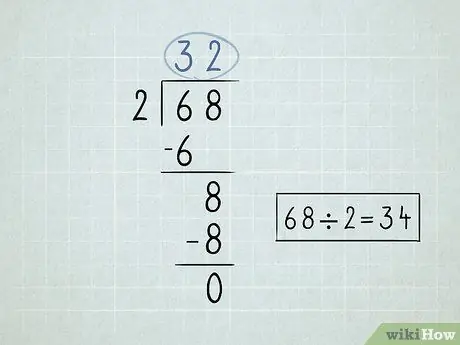
Schritt 2. Schreiben Sie Ihr Divisionsproblem auf

Teilen Sie die Zahl links vom Divisionssymbol oder Divisor durch die erste Zahl unter dem Divisorsymbol. Da 6 / 2 = 3, würden Sie die Zahl 3 über dem Divisionssymbol schreiben.
Multiplizieren Sie die Zahl über dem Divisionssymbol mit dem Divisor. Bringen Sie das Ergebnis bis zum unteren Rand der ersten Zahl unter dem Divisionssymbol. Da 3 x 2 = 6, dann senken Sie die Zahl 6 nach unten.
Subtrahiere die 2 notierten Zahlen. 6 - 6 = 0. Sie können 0 leer lassen, da Sie Zahlen im Allgemeinen nicht mit 0 beginnen.
Bringen Sie die zweite Zahl unter dem Divisionssymbol nach unten.
Teilen Sie die Zahl, die Sie nach unten bringen, durch den Divisor. In diesem Fall ist 8 / 2 = 4. Schreiben Sie die Zahl 4 über das Divisionssymbol.
Multiplizieren Sie die obere rechte Zahl mit dem Divisor und bringen Sie die Zahl nach unten. 4x2 = 8.
Subtrahiere diese Zahlen. Die letzte Subtraktion gibt Null zurück, was bedeutet, dass Sie das Problem gelöst haben. 68 x 2 = 34.

Schritt 3. Berechnen Sie auch den Rest

Einige der Teiler sind nicht vollständig in andere Zahlen unterteilt. Wenn Sie die letzte Subtraktion abgeschlossen haben und keine weiteren Zahlen ableiten müssen, ist die letzte Zahl der Rest.