- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:12.
- Zuletzt bearbeitet 2025-01-23 12:15.
Es gibt verschiedene Möglichkeiten, die Aufteilung vorzunehmen. Sie können Dezimalzahlen, Brüche oder sogar Exponenten dividieren und eine lange oder kurze Division verwenden. Wenn Sie die verschiedenen Methoden zum Teilen von Zahlen kennenlernen möchten, führen Sie die folgenden Schritte aus.
Schritt
Methode 1 von 5: Durchführen einer Division in langen Serien

Schritt 1. Schreiben Sie die Fragen auf
Um eine lange Division durchzuführen, platzieren Sie den Nenner (die Zahl, die geteilt wird) außerhalb des Teilerstrichs und den Zähler (die zu teilende Zahl) innerhalb des Teilerstrichs.
Zum Beispiel: 136÷3

Schritt 2. Teilen Sie die erste Ziffer des Zählers durch den Nenner (wenn möglich)
In diesem Beispiel ist 1 nicht durch 3 teilbar, also setzen Sie eine 0 über den Teilerbalken und fahren Sie mit dem nächsten Schritt fort. Subtrahiere 1 von 0 und setze das Ergebnis unter die Zahl 1.

Schritt 3. Teilen Sie die Restzahl der ersten Ziffer des Zählers und der zweiten Ziffer des Zählers durch den Nenner
Da 1 nicht durch 3 geteilt werden kann, wird weiterhin die Zahl 1 verwendet. Sie müssen 3 subtrahieren. Jetzt dividieren Sie 13 durch 3. Da 3 x 4 = 12, setzen Sie die 4 über den Teilerbalken (rechts von 0), subtrahieren Sie dann 13 durch 12 und schreiben Sie das Ergebnis darunter.

Schritt 4. Teilen Sie die restlichen Zahlen durch den Nenner
Verringere die Zahl 6 rechts von 1, um 16 zu erhalten. Teile jetzt 16 durch 3. Da 3 x 5 = 15, schreibe die Zahl 5 rechts von der Zahl 4, subtrahiere 16 von 15 und schreibe das Ergebnis (16-15= 1) darunter.

Schritt 5. Schreiben Sie den Rest neben den Quotienten
Ihre endgültige Antwort ist 45, wobei 1 übrig bleibt, oder 45 R1.
Methode 2 von 5: Kurze Divisionen durchführen

Schritt 1. Schreiben Sie die Fragen auf
Schreiben Sie den Nenner (die zu teilende Zahl) außerhalb des Teilerstrichs und den Zähler (die zu teilende Zahl) innerhalb des Teilerstrichs. Beachten Sie, dass bei einer kurzen Division der Nenner nicht aus mehr als einer Ziffer bestehen kann.
Zum Beispiel 518 4

Schritt 2. Teilen Sie die erste Ziffer des Zählers durch den Nenner
5 4 = 1 R1. Platzieren Sie den Quotienten (1) über der langen Trennleiste. Schreibe den Rest über die erste Ziffer des Zählers. Platziere eine kleine 1 über 5, um dich daran zu erinnern, dass du noch 1 übrig hast, wenn du 5 durch 4 teilst. Die 518 sollte jetzt so aussehen: 5118

Schritt 3. Dividiere die aus dem Rest und der zweiten Ziffer des Zählers gebildete Zahl durch den Nenner
Die nächste Zahl ist 11, die sich aus dem Restwert (1) und der zweiten Ziffer des Zählers (1) ergibt. 11 4 = 2 R 3 weil 4 x 2 = 8 mit Rest 3. Schreiben Sie den Restwert über die zweite Ziffer des Zählers. Setze 3 über 1. Der anfängliche Zähler (518) sieht nun so aus: 51138

Schritt 4. Teilen Sie die restlichen Zahlen durch den Nenner
Die verbleibende Zahl ist 38; die Zahl 3 stammt aus dem Rest der vorherigen Stufe und 8 ist die letzte Ziffer des Zählers. Berechnen Sie 38 4 = 9 R2. Da 4 x 9 = 36, schreiben Sie "R2" über den Teilungsstrich, denn 38 - 36 = 2.

Schritt 5. Schreiben Sie die endgültige Antwort auf
Das Endergebnis und der Quotient liegen über dem Teilerbalken. Die Antwort lautet 518 4 = 129 R2.
Methode 3 von 5: Brüche dividieren

Schritt 1. Schreiben Sie die Fragen auf
Um einen Bruch zu teilen, notieren Sie einfach den ersten Bruch, gefolgt vom Divisionssymbol und dann den zweiten Bruch.
Zum Beispiel: 3/4 5/8

Schritt 2. Kehren Sie Zähler und Nenner des zweiten Bruchs um
Der zweite Bruch ist jetzt reziprok.
Beispiel: 3/4 8/5

Schritt 3. Ändern Sie das Teilungssymbol in das Zeitsymbol
Um einen Bruch zu teilen, multiplizieren Sie den ersten Bruch mit dem Kehrwert des zweiten.
Beispiel: 3/4 x 8/5
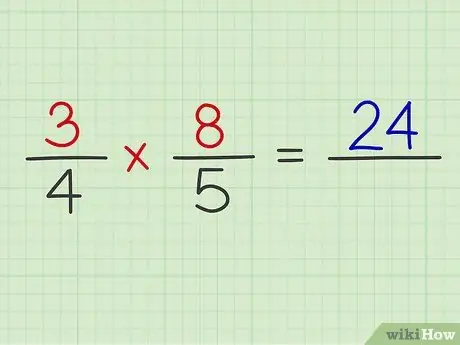
Schritt 4. Multiplizieren Sie den Zähler beider Brüche
Machen Sie es einfach wie die Multiplikation zweier regulärer Brüche.
Beispiel: 3 x 8 = 24
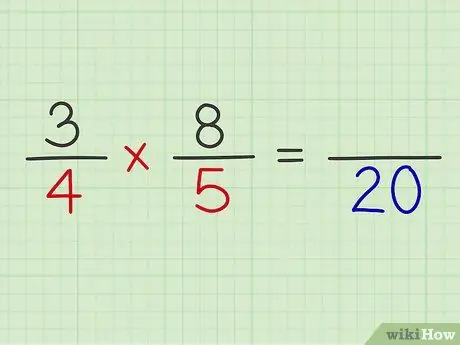
Schritt 5. Multiplizieren Sie die Nenner beider Brüche
Vervollständigen Sie die Berechnung, indem Sie die beiden Brüche multiplizieren.
Beispiel: 4 x 5 = 20
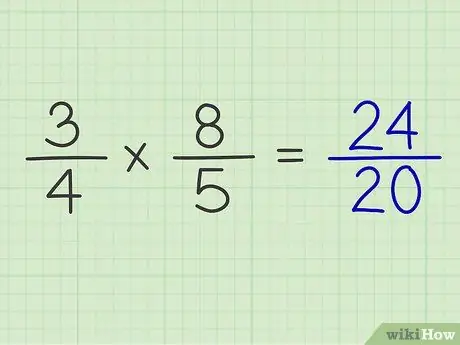
Schritt 6. Setzen Sie das Produkt des Zählers über das Produkt des Nenners
Nach der Multiplikation von Zähler und Nenner der beiden Brüche erhalten Sie das Ergebnis der Berechnung beider Brüche.
Beispiel: 3/4 x 8/5 = 24/20

Schritt 7. Brüche vereinfachen
Um den größten gemeinsamen Faktor zu finden, oder die größte Zahl, die Zähler und Nenner gleichmäßig teilt. In diesem Fall ist der größte gemeinsame Faktor von 24 und 20 4. Um dies zu beweisen, schreiben Sie alle Zähler und Nenner auf und kreisen Sie die Anzahl der größten gemeinsamen Faktoren von beiden ein.
- 24: 1, 2, 3, 4, 6, 8, 12, 24
-
20: 1, 2, 4, 5, 10, 20
- Da 4 der größte gemeinsame Faktor von 24 und 20 ist, dividieren Sie einfach die beiden Zahlen durch 4, um den Bruch zu vereinfachen.
- 24/4 = 6
- 20/4 = 5
- 24/20 = 6/5

Schritt 8. Schreiben Sie den Bruch als gemischte Zahl um (optional)
Der Trick, dividiere einfach den Zähler durch den Nenner und schreibe das Ergebnis als ganze Zahl. Danach schreibe den Rest der Division als neuen Zähler und der Nenner des Bruches ändert sich nicht. Da 6 geteilt durch 5 ergibt 1 mit Rest 1 schreibe die ganze Zahl 1, gefolgt vom neuen Zähler 1, dann den Nenner 5, um eine gemischte Zahl 1 1/5 zu erhalten.
Beispiel: 6/5 = 1 1/5
Methode 4 von 5: Exponenten dividieren

Schritt 1. Stellen Sie sicher, dass die Exponenten/Potenzen dieselbe Basiszahl haben
Exponenten können nur geteilt werden, wenn sie die gleiche Basiszahl haben. Andernfalls können Sie versuchen, sie zu manipulieren, bis Sie dieselbe Basisnummer erhalten.
Beispiel: x8 x5

Schritt 2. Subtrahieren Sie den Exponenten
Sie können den ersten Exponenten einfach vom zweiten subtrahieren. Kümmere dich vorerst nicht um die Basiszahlen.
Beispiel: 8 - 5 = 3
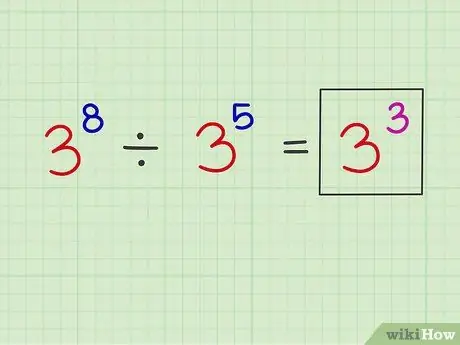
Schritt 3. Platzieren Sie den neuen Exponenten über der ursprünglichen Basiszahl
Jetzt können Sie den neuen Exponenten über die ursprüngliche Basiszahl schreiben.
Beispiel: x8 x5 = x3
Methode 5 von 5: Dezimalzahlen dividieren

Schritt 1. Schreiben Sie die Fragen auf
Schreiben Sie den Nenner (die zu teilende Zahl) außerhalb des Teilerstrichs und den Zähler (die zu teilende Zahl) innerhalb des Teilerstrichs. Bei der Dezimaldivision besteht Ihr Ziel darin, eine Dezimalzahl in eine ganze Zahl umzuwandeln.
Beispiel: 65,5,5

Schritt 2. Ändern Sie den Nenner in eine ganze Zahl
Schieben Sie einfach den Dezimalpunkt um eine Stelle nach rechts, um 0,5 in 5 zu ändern, auch bekannt als 5, 0.

Schritt 3. Ändern Sie den Zähler, indem Sie den Dezimalpunkt um die gleiche Anzahl Stellen wie den Nenner verschieben
Da Sie den Dezimalpunkt des Zählers um eine Stelle nach rechts verschieben, sodass er eine ganze Zahl wird, wird auch der Dezimalpunkt des Nenners um eine Stelle nach rechts verschoben, sodass sich aus 65,5 655 ändert.
Wenn Sie den Dezimalpunkt des Zählers über alle Ziffern hinaus verschieben, müssen Sie bei jeder Verschiebung des Dezimalpunkts Nullen zu den Ziffern hinzufügen. Wird beispielsweise der Dezimalpunkt 7, 2 um drei Stellen nach rechts verschoben, ändert sich die Zahl auf 7,200, da die zweistellige Leerstelle mit Nullen aufgefüllt wird

Schritt 4. Platzieren Sie den Dezimalpunkt auf der langen Teilungsleiste direkt über dem Dezimalpunkt im Zähler
Da Sie den Dezimalpunkt um eine Stelle verschieben, um 0,5 zu einer ganzen Zahl zu machen, ist es eine gute Idee, den Dezimalpunkt über dem Teilungsstrich genau dort zu platzieren, wo der Dezimalpunkt verschoben wird, d. h. nach der letzten 5 in 655.

Schritt 5. Lösen Sie das Problem mit einer einfachen langen Division
Um 655 durch 5 zu teilen, sind die Schritte:
- Teilen Sie die Hunderterstelle des Zählers (6) durch den Nenner (5). Das Ergebnis ist 1 mit einem Rest von 1. Schreiben Sie die Zahl 1 über den Teilerbalken und schreiben Sie 5 unter die Zahl 6, die abgezogen werden soll.
- Der Rest von 1 wird von der Zehnerstelle des Zählers (5) abgezogen, so dass Sie jetzt 15 erhalten. Teilen Sie 15 durch 5, um 3 zu erhalten. Schreiben Sie 3 über den Teilerbalken rechts von 1.
- Lassen Sie die letzten 5 Ziffern weg. Teilen Sie 5 durch 5, um 1 zu erhalten. Schreiben Sie die Zahl 1 über den Teilerbalken rechts von der Zahl 3. Es gibt keinen Rest, da 5 durch 5 teilbar ist.
- Die Antwort der langen sequentiellen Division lautet 655 5 = 131. Dieses Ergebnis entspricht der Antwort auf die Fragen 65,5 0,5.






