3 Möglichkeiten, die Geschwindigkeit zu berechnen

2024 Autor: Jason Gerald | [email protected]. Zuletzt bearbeitet: 2024-01-16 19:19

Geschwindigkeit ist eine Berechnung dafür, wie schnell sich etwas gleichzeitig bewegt. Wenn Sie schon einmal auf den Tacho eines fahrenden Autos geschaut haben, sehen Sie die Geschwindigkeitsanzeige – je weiter die Nadel fährt, desto höher ist die Geschwindigkeit des Fahrzeugs. Es gibt verschiedene Möglichkeiten, die Geschwindigkeit zu berechnen, abhängig von der Art der Informationen, die Sie haben. Im Allgemeinen ist die Formel Geschwindigkeit = Distanz/Zeit (oder k = j/w) ist der einfachste Weg, um die Geschwindigkeit zu berechnen.

Schritt

Methode 1 von 3: Verwenden von Standardgeschwindigkeitsberechnungsformeln

Schritt 1. Ermitteln Sie die Entfernung, die ein Objekt zurückgelegt hat

Die grundlegende Formel, die die meisten Leute verwenden, um die Geschwindigkeit von etwas zu bestimmen, ist sehr einfach zu verwenden. Zunächst einmal müssen Sie wissen, „wie weit das Messobjekt zurückgelegt hat“. Mit anderen Worten, wie groß ist der Abstand zwischen dem Startpunkt und dem Endpunkt des Objekts?

Diese Formel ist anhand eines Beispiels leichter zu verstehen. Nehmen wir an, wir fahren mit dem Auto zu einem Spielplatz für "161 Kilometer". In wenigen Schritten können wir diese Informationen verwenden, um die Berechnung der Formel abzuschließen

Schritt 2. Ermitteln Sie die Zeit, die das Objekt benötigt, um diese Entfernung zurückzulegen

Die nächste Information, die Sie benötigen, ist, wie lange das Objekt braucht, um eine bestimmte Entfernung zu erreichen. Mit anderen Worten, wie lange dauert es, bis sich das Objekt vom Startpunkt zum Endpunkt bewegt?

Nehmen wir in diesem Beispiel an, dass das Objekt ca. zwei Stunden um ans Ziel zu kommen.

Schritt 3. Dividieren Sie die Entfernung durch die Zeit, die benötigt wird, um die Geschwindigkeit des Objekts zu ermitteln

Sie benötigen nur diese beiden Informationen, um die Geschwindigkeit des Objekts zu kennen. Die Distanz zur Zeit ist gleich der Geschwindigkeit des Objekts.

In diesem Beispiel 161 Kilometer/2 Stunden = 80,5 Kilometer/Stunde.

Schritt 4. Vergessen Sie nicht das verwendete Gerät

Es ist sehr wichtig, dass Sie bei Ihrer Antwort die richtigen Einheiten verwenden (z. B. Kilometer pro Stunde usw.). Ohne diese Einheiten ist es für die Leute sehr schwierig, die Bedeutung Ihrer Antwort zu verstehen. Sie können auch Punkte verlieren, wenn Sie bei Schulaufgaben die falsche Einheit verwenden.

Die Einheit der Geschwindigkeit ist Entfernungseinheit zu Zeiteinheit. Da wir beispielsweise die Entfernung in Kilometern und die Zeit in Stunden messen, sind die verwendeten Einheiten Kilometer/Stunde (oder Kilometer pro Stunde).

Methode 2 von 3: Schwierigere Berechnungen lösen

Schritt 1. Finden Sie mehrere verschiedene Variablen, um das Problem von Entfernung und Zeit zu lösen

Sobald Sie die Grundformel für Geschwindigkeit verstanden haben, können Sie damit andere Berechnungen als die Geschwindigkeit durchführen. Wenn Sie beispielsweise zunächst nur die Geschwindigkeit des Objekts und eine andere Variable kennen, können Sie die obige Formel neu anordnen, um die unbekannten Informationen zu finden.

• Nehmen wir zum Beispiel an, wir wissen, dass ein Zug vier Stunden lang mit 20 Stundenkilometern fährt, aber wir wissen nicht, wie weit er gefahren ist. Um das herauszufinden, können wir die Formel wie folgt neu anordnen:

  Geschwindigkeit = Distanz/Zeit

  Geschwindigkeit × Zeit = (Entfernung/Zeit) × Zeit

  Geschwindigkeit × Zeit = Entfernung

  20 km/h × 4 Stunden = Distanz = 80 Kilometer

Schritt 2. Konvertieren Sie die von Ihnen verwendeten Einheiten nach Bedarf

Manchmal kann es vorkommen, dass Sie die Geschwindigkeit mit einer bestimmten Einheit berechnen, diese jedoch in eine andere Einheit umrechnen müssen. In diesem Fall müssen Sie einen Umrechnungsfaktor verwenden, um die Antwort in den richtigen Einheiten zu erhalten. Schreiben Sie dazu einfach die Beziehung zwischen den Einheiten in Bruchform und multiplizieren Sie. Beim Multiplizieren den Bruch nach Bedarf umkehren, um unerwünschte Einheiten zu entfernen. Diese Methode ist viel einfacher als sie klingt!

• Nehmen wir zum Beispiel an, dass wir in der obigen Beispielaufgabe die Antwort in Meilen statt in Kilometern benötigen. Eine Meile entspricht etwa 1,6 Kilometern. Wir können die Konvertierung also wie folgt durchführen:

  80 Kilometer × 1,6 Kilometer = 50 Meilen

• Denken Sie daran, da Kilometer am unteren Rand des Bruchs angezeigt werden, werden Kilometer aus der vorherigen Antwort entfernt, sodass das Endergebnis Meilen verwendet.
• Diese Website bietet Umrechnungsfunktionen für die meisten der am häufigsten verwendeten Einheiten.

Schritt 3. Ersetzen Sie die Variable "distanz" nach Bedarf durch die Distanzformel

Objekte bewegen sich nicht immer auf einem geraden, glatten Pfad. Wenn dies der Fall ist, können Sie möglicherweise nicht einfach einen numerischen Wert als Entfernungseinheit in die Standardgeschwindigkeitsformel eingeben. Möglicherweise müssen Sie jedoch den Buchstaben j in der Formel k = j/w durch eine Formel ersetzen, die der vom Objekt zurückgelegten Entfernung ähnelt.

• Nehmen wir zum Beispiel an, ein Flugzeug dreht sich fünfmal über eine Distanz von 32 km durch die Luft. Das Flugzeug absolvierte die Runde in einer halben Stunde. In diesem Beispiel müssen wir noch die Gesamtstrecke ermitteln, die das Flugzeug zurückgelegt hat, bevor wir seine Geschwindigkeit bestimmen können. Wir können die Formel zur Berechnung der Entfernung um einen Kreis (Entfernung um ihn herum) anstelle von j in dieser Formel verwenden. Diese Formel lautet Umfang = 2πr wobei r = Kreisradius. So lösen Sie es:

  k = (2 × × r)/w

  k = (2 × × 10)/0,5

  k = 62,83/0,5 = 125,66 Meilen/Stunde

Schritt 4. Verstehen Sie, dass k = j/w die durchschnittliche Geschwindigkeit angibt

Die einfache und einfache Formel, die wir verwenden, um die Geschwindigkeit zu bestimmen, hat einen Nachteil. Der resultierende Wert ist technisch die Durchschnittsgeschwindigkeit. Dies bedeutet, dass die Formel davon ausgeht, dass das zu messende Objekt dieselbe Geschwindigkeit verwendet, wenn es sich bewegt. Wie wir weiter unten sehen werden, wird es viel schwieriger sein, die Geschwindigkeit eines Objekts in einem einzigen Moment zu bestimmen.

Um diesen Unterschied zu veranschaulichen, stellen Sie sich vor, wann Sie das letzte Mal mit dem Auto gefahren sind. Es ist unwahrscheinlich, dass Sie mit der gleichen Geschwindigkeit reisen, wie Sie reisen. Sie beginnen Ihre Fahrt jedoch normalerweise mit niedriger Geschwindigkeit und erhöhen Ihre Geschwindigkeit allmählich, wobei Sie aufgrund von roten Ampeln, Staus usw. anhalten. Wenn Sie die Standardgeschwindigkeitsformel verwenden, um die Geschwindigkeit während der Fahrt zu ermitteln, können Änderungen dieser Geschwindigkeit nicht erkannt werden. Sie erhalten jedoch eine Antwort, die die Durchschnittsgeschwindigkeit aller Geschwindigkeitsunterschiede anzeigt, die Sie zurücklegen

Methode 3 von 3: Berechnung der Momentangeschwindigkeit

Notiz:

In diesem Abschnitt werden Techniken verwendet, die Personen, die sich noch nie mit Infinitesimalrechnung beschäftigt haben, weniger vertraut sind. Lesen Sie unsere Artikel über Infinitesimalrechnung, um Hilfe zu erhalten.

Schritt 1. Verstehen Sie, dass Geschwindigkeit als Beschleunigungsrate definiert ist

Geschwindigkeitsberechnungen auf hoher Ebene sind ziemlich verwirrend, weil Mathematiker und Wissenschaftler unterschiedliche Definitionen verwenden, um "Geschwindigkeit" und "Beschleunigung" zu beschreiben. Beschleunigung hat zwei Komponenten: eine "Rate" und eine "Richtung". Die Geschwindigkeit entspricht der Geschwindigkeit des Objekts. Eine Richtungsänderung bewirkt eine Beschleunigungsänderung, jedoch keine Geschwindigkeitsänderung.

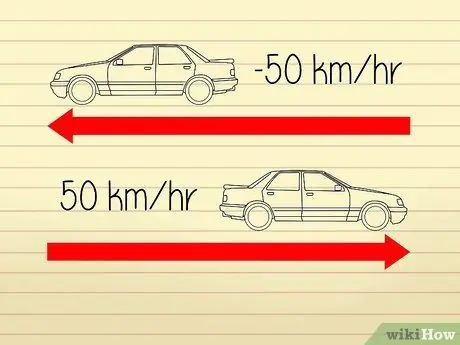
• Nehmen wir zum Beispiel an, dass sich zwei Autos in entgegengesetzte Richtungen bewegen. Die Tachos beider Autos zeigen eine Zahl von 50 km/h an, beide fahren also mit der gleichen Geschwindigkeit. Da sich die Autos jedoch voneinander entfernen, können wir sagen, dass eines der Autos eine "Beschleunigung" von -50 km/h hat, während das andere eine "Beschleunigung" von 50 km/h hat.
• Genau wie Berechnungen der Momentangeschwindigkeit können Sie auch Berechnungen der Momentanbeschleunigung durchführen.

Schritt 2. Verwenden Sie absolute Werte, um die negative Beschleunigung zu messen

Ein Objekt kann eine negative Beschleunigungsrate haben (wenn es sich relativ zu einem anderen Objekt in eine negative Richtung bewegt). Es gibt jedoch keine negative Geschwindigkeit. In diesem Fall gibt der Absolutwert der Rate also die Geschwindigkeit des Objekts an.

Aus diesem Grund haben im obigen Beispielproblem beide Autos eine Geschwindigkeit von 50km/h.

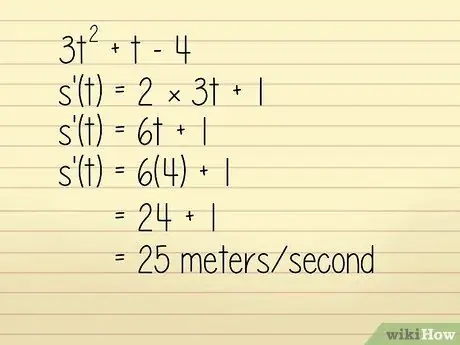
Schritt 3. Nehmen Sie die Ableitung der Position der Funktion

Wenn Sie eine Funktion k(w) haben, die die Position eines Objekts anzeigt, ohne die Zeit berechnen zu müssen, zeigt die Ableitung von k(w) die Beschleunigung an, ohne dass eine Zeitmessung erforderlich ist. Setzen Sie einfach den Zeitwert in diese Formel ein, damit die Variable w (oder welcher Zeitwert auch immer verwendet wird) entsprechend dieser Zeit beschleunigt wird. Von hier aus können Sie leicht die Geschwindigkeit des Objekts ermitteln.

• Nehmen wir zum Beispiel an, dass die Position eines Objekts in einem Meter in der Gleichung 3q. beschrieben wird² + w - 4 wobei w = Zeit in Sekunden. Wir wollen die Geschwindigkeit des Objekts bei w = 4 Sekunden wissen. In diesem Fall können Sie es lösen, indem Sie:

  3w² +w - 4

  k'(w) = 2 × 3w + 1

  k'(w) = 6w + 1

• Nun geben wir w = 4 ein:

  k'(w) = 6(4) + 1 = 24 + 1 = 25 Meter/Sekunde. Technisch ist dies eine Beschleunigungsberechnung, aber da sie positiv ist und die Richtung in der Frage nicht erwähnt wird, können wir sie verwenden, um die Geschwindigkeit zu ermitteln.

Schritt 4. Nehmen Sie die integrale Beschleunigungsfunktion

Beschleunigung ist eine Methode, um die Änderung der Beschleunigung eines Objekts im Laufe der Zeit zu messen. Dieses Thema ist zu komplex, um in diesem Artikel vollständig erklärt zu werden. Es ist jedoch nützlich zu beachten, dass das Integral von a(w) das Ergebnis der Beschleunigung basierend auf dieser Zeit zurückgibt, wenn Sie eine Funktion a(w) haben, die die Beschleunigung in Bezug auf die Zeit darstellt. Denken Sie daran, dass es sehr nützlich ist, die Anfangsbeschleunigung eines Objekts zu kennen, damit Sie die Konstante dieses Ergebnisses aus einem unendlichen Integral definieren können.

• Angenommen, ein Objekt hat eine konstante Beschleunigung (in m/s² als Ergebnis von a(w) = -30. Sagen Sie auch, dass das Objekt eine Anfangsbeschleunigung von 10 m/s hat. Wir müssen die Geschwindigkeit bei w = 12 Sekunden finden. In diesem Fall können wir es lösen durch:

  a(w) = -30

  p(w)= a(w)dw = -30dw = -30w + C

• Um C zu finden, lösen wir p(w) nach w = 0 auf. Denken Sie daran, dass die Anfangsbeschleunigung des Objekts 10 m/s beträgt.

  p(0) = 10 = -30(0) + C

  10 = C, also p(w) = -30w + 10

• Nun können wir w = 12 Sekunden eingeben.

  p(12) = –30(12) + 10 = –360 + 10 = –350. Da die Geschwindigkeit ein absoluter Wert der Beschleunigung ist, ist die Geschwindigkeit des Objekts 350 Meter/Sekunde.

Tipps

• Übung macht groß! Versuchen Sie, Ihre eigene Frage zu erstellen, indem Sie die Zahlen in der obigen Beispielaufgabe ersetzen.
• Wenn Sie nach einer schnellen Methode suchen, um das Rechnen für eine bessere Berechnungsgeschwindigkeit zu üben, verwenden Sie den Online-Derivate-Rechner hier und den Online-Integral-Rechner hier.